题目内容
设函数f(x)是定义域在(-∞,+∞)上的增函数,如果不等式f(1-ax-x2)＜f(2-a)对于任意x∈［0,1］都成立.求实数a的取值范围.
解:∵f(x)在(-∞,+∞)上为增函数.
∴不等式f(1-ax-x2)＜f(2-a)可化为1-ax-x2＜2-a,即x2+ax+1-a＞0在x∈［0,1］上恒成立.
令g(x)=x2+ax+1-a=(x+
)2-
-a+1,x∈［0,1］,
则此问题转化为g(x)在［0,1］上的最小值大于0.
(1)
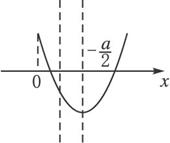
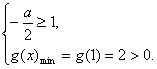
∴a≤-2合题意.
(2)
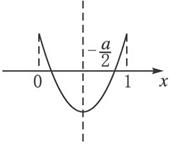
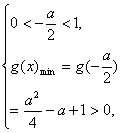
即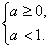
即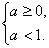
∴-2＜a＜0合题意.
(3)
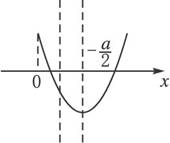
即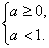
即
∴0≤a＜1合题意.
综(1)(2)(3)得 a＜1.
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
相关题目
f(-1-log3
=1 (n∈N*)
)
的单调递减区间.