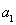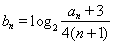题目内容
20.已知正项数列![]() ,其前n项和Sn满足10Sn=an2+5an+6,且a1,a3,a15成等比数列,求数列
,其前n项和Sn满足10Sn=an2+5an+6,且a1,a3,a15成等比数列,求数列![]() 的通项an.
的通项an.
∵10Sn=an2+5an+6, ①
∴10a1=a12+5a1+6, 解之得a1=2或a1=3.
又10Sn-1=an-12+5an-1+6(n≥2), ②
由①-②得
10an=(an2-a n-12)+5(an-an-1),
即(an+an-1)(an-an-1-5)=0.
∵an+an-1>0,
∴an-an-1=5(n≥2).
当a1=3时,a2=13,an=73,a1,a2,an不成等比数列,a1≠3.
当a1=2时,a2=12,an=72,有a32=a1a2,
∴a1=2,∴an=5n-3.

练习册系列答案
相关题目