题目内容
已知向量a
 ,b
,b
 ,c
,c

 ,其中
,其中 .
.
(1)若 ,求函数
,求函数 b·c的最小值及相应的
b·c的最小值及相应的 的值;
的值;
(2)若a与b的夹角为 ,且a⊥c,求
,且a⊥c,求 的值.
的值.
(1)函数 的最小值为
的最小值为 ,相应的
,相应的 的值为
的值为
(2)
解析试题分析:(1)由已知易求得 ,此时再换元令
,此时再换元令  可得
可得 ,即可求得
,即可求得 ,然后再反求此时对应的
,然后再反求此时对应的 的值,可得结果.
的值,可得结果.
(2)利用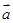 与
与 的夹角为
的夹角为 ,可求得
,可求得 ,再根据
,再根据 可得
可得 ,然后联立两式即可求得结果.
,然后联立两式即可求得结果.
试题解析:(1)
 ,又
,又

令 则
则 ,且
,且

 当
当 时,
时, ,此时
,此时
即 ,
,
又 ,
,
 ,即
,即
所以函数 的最小值为
的最小值为 ,相应的
,相应的 的值为
的值为 .
.
(2)
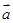 与
与 的夹角为
的夹角为 ,
, .
. ,
, ,即
,即
又 ,
, .
.
化简得 .将
.将 代入可得
代入可得 ,
, .
.
考点:三角恒等变换;换元法求最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,求
,求 的值
的值





 的最小正周期和单调递减区间;
的最小正周期和单调递减区间; 中,
中, 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若 ,求
,求 ,并写出函数
,并写出函数 的最小正周期;
的最小正周期; 为非零常数,且
为非零常数,且 ,试问
,试问 是周期函数吗?证明你的结论.
是周期函数吗?证明你的结论. ,则行列式
,则行列式
 的终边过
的终边过 (
( ),则
),则 的值为__________.
的值为__________. ,若
,若 ,则
,则
 .
. ,
, ,则
,则
 .
.