题目内容
图1-1-12，已知在△ABC中，D是AC的中点，DE∥BC交AB于点E，EF∥AC交BC于点F.求证:BF=CF.
图1-1-12
思路分析：根据D是AC的中点，利用平行，得到E是AB的中点，再利用平行即可得到F是BC的中点.
证明：在△ABC中，∵D是AC的中点，DE∥BC，
∴E是AB的中点(经过三角形一边的中点与另一边平行的直线必平分第三边).
又∵EF∥AC交BC于F，∴F是BC的中点，即BF=FC.
深化升华 在三角形中，只要给了一边的中点和平行线，根据平行线等分线段定理的推论2，就可得出平行线与另一边的交点即是中点.本题也可以利用平行四边形和全等形来证明，但会显得麻烦.
练习册系列答案
名校课堂系列答案
相关题目
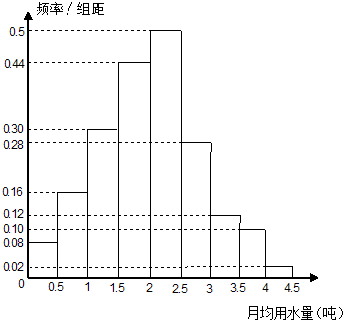我国是世界上严重缺水的国家之一，城市缺水问题较为突出．某市政府为了节约生活用水，计划在本市试行居民生活用水定额管理，为此市政府首先采用抽样调查的方法获得了n位居民某年的月均用水量（单位：吨）．根据所得的n个数据按照区间[0，0.5），[0.5，1），[1，1.5），[1.5，2），[2，2.5），[2.5，3），[3，3.5），[3.5，4），[4，4.5]进行分组，得到频率分布直方图如图
