题目内容
已知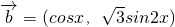 ,
,
(1)若 ,求tan x;
,求tan x;
(2)若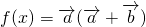 ,求f(x)的最大值.
,求f(x)的最大值.
解:(1)∵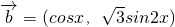 ,
, ,
, ,
,
∴ ,…(3分)∴
,…(3分)∴ .…(6分)
.…(6分)
(2)∵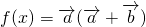 =
= …(7分)
…(7分)
=1+ …(8分)
…(8分)
=1+2 =1+2
=1+2 ,…(10分)
,…(10分)
∴当 =1时,f(x)有最大值3. …(12分)
=1时,f(x)有最大值3. …(12分)
分析:(1)利用两个向量共线的性质可得 ,由此求得tan x的值.
,由此求得tan x的值.
(2)由于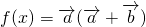 ,利用两个向量的数量积公式、两角和差的正弦公式化简函数的解析式为1+2
,利用两个向量的数量积公式、两角和差的正弦公式化简函数的解析式为1+2 ,由此求得函数的最大值.
,由此求得函数的最大值.
点评:本题主要考查两个向量的数量积公式的应用,两个向量共线的性质,两个向量坐标形式的运算,正弦函数的值域,属于中档题.
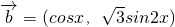 ,
, ,
, ,
,∴
 ,…(3分)∴
,…(3分)∴ .…(6分)
.…(6分)(2)∵
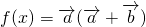 =
= …(7分)
…(7分)=1+
 …(8分)
…(8分)=1+2
 =1+2
=1+2 ,…(10分)
,…(10分)∴当
 =1时,f(x)有最大值3. …(12分)
=1时,f(x)有最大值3. …(12分)分析:(1)利用两个向量共线的性质可得
 ,由此求得tan x的值.
,由此求得tan x的值.(2)由于
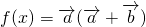 ,利用两个向量的数量积公式、两角和差的正弦公式化简函数的解析式为1+2
,利用两个向量的数量积公式、两角和差的正弦公式化简函数的解析式为1+2 ,由此求得函数的最大值.
,由此求得函数的最大值.点评:本题主要考查两个向量的数量积公式的应用,两个向量共线的性质,两个向量坐标形式的运算,正弦函数的值域,属于中档题.

练习册系列答案
相关题目
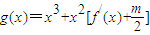 在区间(t,3)上有最值,求实数m取值范围;
在区间(t,3)上有最值,求实数m取值范围;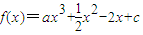
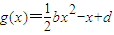 ,在(1)的条件下,是否存在实数b,使得函数g(x)的图象与函数f(x)的图象恒有含x=-1的三个不同交点?若存在,求出实数b的取值范围;否则说明理由.
,在(1)的条件下,是否存在实数b,使得函数g(x)的图象与函数f(x)的图象恒有含x=-1的三个不同交点?若存在,求出实数b的取值范围;否则说明理由.
 ;
;  在区间(—1,1)上是增函数,求t的取值范围。
在区间(—1,1)上是增函数,求t的取值范围。 .
. ,求t.
,求t.