题目内容
能够把圆O:x2+y2=16的周长和面积同时分为相等的两部分的函数称为圆O的“和谐函数”,下列函数不是圆O的“和谐函数”的是
- A.f(x)=4x3+x
- B.

- C.

- D.f(x)=ex+e-x
D
分析:由“和谐函数”的定义及选项知,该函数若为“和谐函数”,其函数须为过原点的奇函数,由此逐项判断即可得到答案.
解答:由“和谐函数”的定义知,若函数为“和谐函数”,则该函数为过原点的奇函数.
A中,f(0)=0,且f(x)为奇函数,故f(x)=4x3+x为“和谐函数”;
B中,f(0)=ln =ln1=0,且f(-x)=ln
=ln1=0,且f(-x)=ln =ln
=ln =-ln
=-ln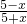 =f(x),所以f(x)为奇函数,
=f(x),所以f(x)为奇函数,
所以f(x)=ln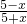 为“和谐函数”;
为“和谐函数”;
C中,f(0)=tan0=0,且f(-x)=tan =-tan
=-tan =f(x),f(x)为奇函数,
=f(x),f(x)为奇函数,
故f(x)=tan 为“和谐函数”;
为“和谐函数”;
D中,f(0)=e0+e-0=2,所以f(x)=ex+e-x的图象不过原点,故f(x))=ex+e-x不为“和谐函数”;
故选D.
点评:本题考查函数的奇偶性、单调性,考查学生对新问题的分析理解能力及解决能力,属中档题.
分析:由“和谐函数”的定义及选项知,该函数若为“和谐函数”,其函数须为过原点的奇函数,由此逐项判断即可得到答案.
解答:由“和谐函数”的定义知,若函数为“和谐函数”,则该函数为过原点的奇函数.
A中,f(0)=0,且f(x)为奇函数,故f(x)=4x3+x为“和谐函数”;
B中,f(0)=ln
 =ln1=0,且f(-x)=ln
=ln1=0,且f(-x)=ln =ln
=ln =-ln
=-ln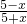 =f(x),所以f(x)为奇函数,
=f(x),所以f(x)为奇函数,所以f(x)=ln
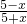 为“和谐函数”;
为“和谐函数”;C中,f(0)=tan0=0,且f(-x)=tan
 =-tan
=-tan =f(x),f(x)为奇函数,
=f(x),f(x)为奇函数,故f(x)=tan
 为“和谐函数”;
为“和谐函数”;D中,f(0)=e0+e-0=2,所以f(x)=ex+e-x的图象不过原点,故f(x))=ex+e-x不为“和谐函数”;
故选D.
点评:本题考查函数的奇偶性、单调性,考查学生对新问题的分析理解能力及解决能力,属中档题.

练习册系列答案
相关题目


