题目内容
已知a为实数,函数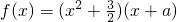 .
.
(I)若函数f(x)的图象上有与x轴平行的切线,求a的取值范围;
(II)当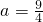 时,对任意x1,x2∈[-1,0],不等式|f(x1)-f(x2)|≤m恒成立,试求m的取值范围.
时,对任意x1,x2∈[-1,0],不等式|f(x1)-f(x2)|≤m恒成立,试求m的取值范围.
解:(I)∵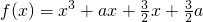 ,∴
,∴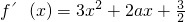
∵函数f(x)的图象上有x轴平行的切线,∴f'(x)=0有实数解∴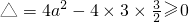 ,∴
,∴
因此,实数a的取值范围是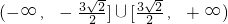 …(5分)
…(5分)
(II)当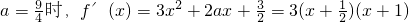
由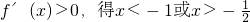 …(6分)
…(6分)
由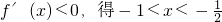
因此,函数f(x)的单调区间为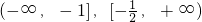 ;
;
单调减区间为 …(8分)
…(8分)
由此可知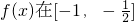 上的最大值为
上的最大值为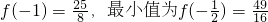 ;
;
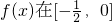 上的最大值为
上的最大值为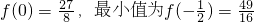 .
.
∴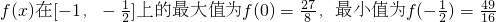 .
.
因此,任意的x1x2∈[-1,0],恒有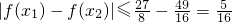
所以m的取值范围是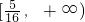 …(12分)
…(12分)
分析:(I)若函数f(x)的图象上有与x轴平行的切线,则f'(x)=0有实数解,从而可求a的取值范围;
(II)对任意x1,x2∈[-1,0],不等式|f(x1)-f(x2)|≤m恒成立,可转化为:对任意x1,x2∈[-1,0],不等式f(x1)max-f(x2)min≤m恒成立,利用导数可求.
点评:本题的考点是利用导数求函数在闭区间上的最值,主要考查导数的几何意义,考查恒成立问题,关键是将不等式恒成立问题转化为最值去解决.
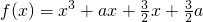 ,∴
,∴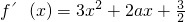
∵函数f(x)的图象上有x轴平行的切线,∴f'(x)=0有实数解∴
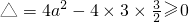 ,∴
,∴
因此,实数a的取值范围是
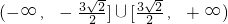 …(5分)
…(5分)(II)当
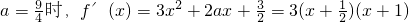
由
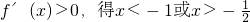 …(6分)
…(6分)由
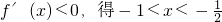
因此,函数f(x)的单调区间为
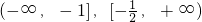 ;
;单调减区间为
 …(8分)
…(8分)由此可知
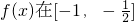 上的最大值为
上的最大值为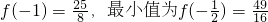 ;
;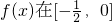 上的最大值为
上的最大值为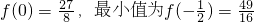 .
.∴
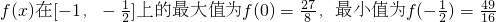 .
.因此,任意的x1x2∈[-1,0],恒有
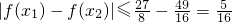
所以m的取值范围是
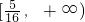 …(12分)
…(12分)分析:(I)若函数f(x)的图象上有与x轴平行的切线,则f'(x)=0有实数解,从而可求a的取值范围;
(II)对任意x1,x2∈[-1,0],不等式|f(x1)-f(x2)|≤m恒成立,可转化为:对任意x1,x2∈[-1,0],不等式f(x1)max-f(x2)min≤m恒成立,利用导数可求.
点评:本题的考点是利用导数求函数在闭区间上的最值,主要考查导数的几何意义,考查恒成立问题,关键是将不等式恒成立问题转化为最值去解决.

练习册系列答案
相关题目