题目内容
如图,已知椭圆![]() 的焦点和上顶点分别为
的焦点和上顶点分别为![]() 、
、![]() 、
、![]() ,
,
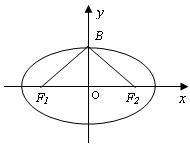 我们称
我们称![]() 为椭圆
为椭圆![]() 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为 椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为 椭圆的相似比.
(1)已知椭圆![]() 和
和![]() ,
,
判断![]() 与
与![]() 是否相似,如果相似则求出
是否相似,如果相似则求出![]() 与
与![]() 的相似比,若不相似请说明理由;
的相似比,若不相似请说明理由;
(2)设短半轴长为![]() 的椭圆
的椭圆![]() 与椭圆
与椭圆![]() 相似,试问在椭圆
相似,试问在椭圆![]() 上是否存在两点
上是否存在两点![]() 、
、![]() 关于直线
关于直线![]() 对称,,若存在求出b的范围,不存在说明理由.
对称,,若存在求出b的范围,不存在说明理由.
解:(1)椭圆![]() 与
与![]() 相似.
相似.
因为椭圆![]() 的特征三角形是腰长为2,底边长为
的特征三角形是腰长为2,底边长为![]() 的等腰三角形
的等腰三角形
而![]() 的特征三角形是腰长为4,底边长为
的特征三角形是腰长为4,底边长为![]() 的等腰三角形,
的等腰三角形,
因此两个等腰三角形相似,且相似比为1:2
(2)椭圆![]() 的方程为:
的方程为:![]() .
.
假定存在,则设![]() 、
、![]() 所在直线为
所在直线为![]() ,
,![]() 中点为
中点为![]() .
.
则
![]() .
. ![]()
所以![]() ,
,![]() .
.
中点在直线![]() 上,所以有
上,所以有![]() . 又中点
. 又中点![]() 在椭圆内
在椭圆内
![]()
![]()

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 的焦点和上顶点分别为F1、F2、B,我们称△F1BF2为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的焦点和上顶点分别为F1、F2、B,我们称△F1BF2为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比. 和
和 判断C2与C1是否相似,如果相似则求出C2与C1的相似比,若不相似请说明理由;
判断C2与C1是否相似,如果相似则求出C2与C1的相似比,若不相似请说明理由;
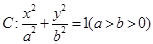 的焦点为
的焦点为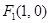 、
、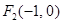 ,离心率为
,离心率为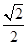 ,过点
,过点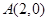 的直线
的直线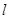 交椭圆
交椭圆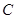 于
于 、
、 两点.
两点.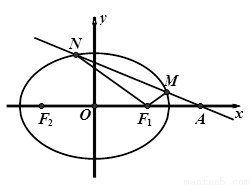
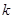 的取值范围;
的取值范围;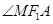 和
和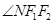 是否总相等?若相等,请给出证明,若不相等,说明理由.
是否总相等?若相等,请给出证明,若不相等,说明理由.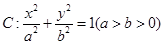 的焦点和上顶点分别为
的焦点和上顶点分别为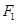 、
、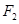 、
、 ,我们称
,我们称 为椭圆
为椭圆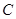 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.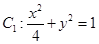 和
和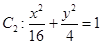 ,判断
,判断 与
与 是否相似,如果相似则求出
是否相似,如果相似则求出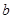 的椭圆为
的椭圆为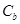 ,且直线
,且直线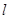 与椭圆为
与椭圆为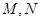 (异于端点),试问:当
(异于端点),试问:当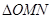 面积最大时,
面积最大时,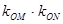 是否与
是否与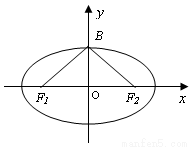
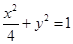 的焦点为
的焦点为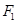 、
、 ,点
,点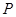 为椭圆上任意一点,过
为椭圆上任意一点,过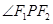 的外角平分线的垂线,垂足为点
的外角平分线的垂线,垂足为点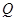 ,过点
,过点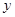 轴的垂线,垂足为
轴的垂线,垂足为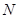 ,线段
,线段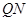 的中点为
的中点为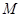 ,则点
,则点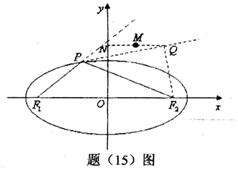
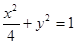 的焦点为F1,F2,点P为椭圆上任意一点,过F2作
的焦点为F1,F2,点P为椭圆上任意一点,过F2作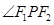 的外角平分线的垂线,垂足为点Q,过点Q作
的外角平分线的垂线,垂足为点Q,过点Q作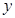 轴的垂线,垂足为N,线段QN的中点为M,则点M的轨迹方程为
。
轴的垂线,垂足为N,线段QN的中点为M,则点M的轨迹方程为
。