题目内容
函数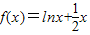 的零点所在的区间是( )
的零点所在的区间是( )A.
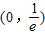
B.(-1,0)
C.
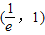
D.(1,+∞)
【答案】分析:由于函数在(0,+∞)单调递增且连续,根据零点判定定理只要满足f(a)f(b)<0即为满足条件的区间;
解答:解:因为函数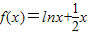 ,(x>0)
,(x>0)
f(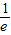 )=ln
)=ln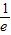 +
+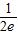 =-1+
=-1+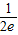 <0,
<0,
f(1)=ln1+ =
= >0,
>0,
∴f(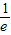 )f(1)<0,根据零点定理可得,
)f(1)<0,根据零点定理可得,
∴函数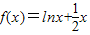 的零点所在的区间(
的零点所在的区间(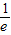 ,1),
,1),
故选C;
点评:此题主要考查函数零点的吧判定定理及其应用,解题的过程中要注意函数的定义域,是一道基础题;
解答:解:因为函数
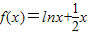 ,(x>0)
,(x>0)f(
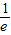 )=ln
)=ln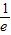 +
+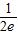 =-1+
=-1+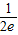 <0,
<0,f(1)=ln1+
 =
= >0,
>0,∴f(
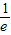 )f(1)<0,根据零点定理可得,
)f(1)<0,根据零点定理可得,∴函数
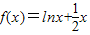 的零点所在的区间(
的零点所在的区间(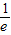 ,1),
,1),故选C;
点评:此题主要考查函数零点的吧判定定理及其应用,解题的过程中要注意函数的定义域,是一道基础题;

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 的零点所在的区间是( )
的零点所在的区间是( ) )
B.(
)
B.( )
C.(
)
C.( )
D.(
)
D.( )
) 的零点所在的区间为( )
的零点所在的区间为( ) ,
, ) B.(-
) B.(- )
) 的零点所在的区间是( )
的零点所在的区间是( ) B.
B. C.
C. D.
D.
 的零点所在的区间为( )
的零点所在的区间为( ) B、
B、 C、
C、 D、
D、
 的零点所在的区间是( )
的零点所在的区间是( ) D.
D.