题目内容
定义在R上的偶函数f(x)满足:对任意的 ,
,
有 ,则当n∈N﹡时,有( ).
,则当n∈N﹡时,有( ).
A. < < < < | B. < < < < |
C. < < < < | D. < < < < |
D
解析试题分析:因为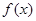 对任意的
对任意的 ,有
,有 所以
所以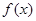 在
在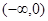 为增函数,又
为增函数,又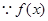 是定义在R上的偶函数,
是定义在R上的偶函数,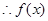 在
在 为减函数,
为减函数,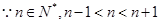 ,所以
,所以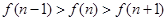 ,即
,即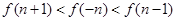 .
.
考点:函数的奇偶性、单调性.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
已知 ,则下列不等式一定成立的是( ).
,则下列不等式一定成立的是( ).
A. | B. | C. | D. |
已知i为虚数单位,复数 ,则复数
,则复数 在复平面上的对应点位于( )
在复平面上的对应点位于( )
| A.第四象限 | B.第三象限 | C.第二象限 | D.第一象限 |
 若
若 是
是 的最小值,则
的最小值,则 的取值范围为( )
的取值范围为( )
| A.[0,2] | B.[-1,2] | C.[1,2] | D.[-1,0] |
已知函数 的周期为2,当
的周期为2,当 ∈[-1,1]时
∈[-1,1]时 ,那么函数
,那么函数 的图象与函数
的图象与函数 的图象的交点共有( ).
的图象的交点共有( ).
| A.10个 | B.9个 | C.8个 | D.1个 |
设函数 ,
, 的定义域都为R,且
的定义域都为R,且 是奇函数,
是奇函数, 是偶函数,则下列结论正确的是( ).
是偶函数,则下列结论正确的是( ).
A.  是偶函数 是偶函数 | B.| | | 是奇函数 是奇函数 |
C. | | |是奇函数 |是奇函数 | D.|  |是奇函数 |是奇函数 |
若函数 是奇函数,则
是奇函数,则 的值为( )
的值为( )
| A.1 | B.2 | C.3 | D.4 |
设偶函数 在
在 上为减函数,且
上为减函数,且 ,则不等式
,则不等式 的解集为( ).
的解集为( ).
A. | B. |
C. | D. |
 ,设P:函数
,设P:函数 在R上递增,Q:复数Z=(
在R上递增,Q:复数Z=( -4) +
-4) +