题目内容
已知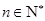 ,数列
,数列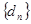 满足
满足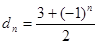 ,数列
,数列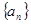 满足
满足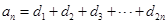 ;又知数列
;又知数列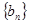 中,
中,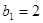 ,且对任意正整数
,且对任意正整数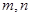 ,
,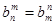 .
.
(Ⅰ)求数列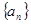 和数列
和数列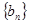 的通项公式;
的通项公式;
(Ⅱ)将数列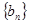 中的第
中的第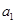 项,第
项,第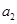 项,第
项,第 项,……,第
项,……,第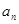 项,……删去后,剩余的项按从小到大的顺序排成新数列
项,……删去后,剩余的项按从小到大的顺序排成新数列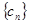 ,求数列
,求数列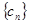 的前
的前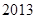 项和.
项和.
【答案】
(1)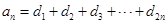
 ,
,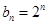
(2)

【解析】
试题分析:解: 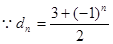 ,
,
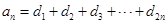
 3分
3分
又由题知:令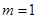 ,则
,则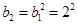 ,
,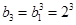
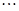
 5分
5分
若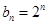 ,则
,则 ,
, ,所以
,所以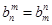 恒成立
恒成立
若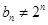 ,当
,当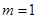 ,
,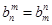 不成立,所以
不成立,所以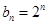 6分
6分
(Ⅱ)由题知将数列 中的第3项、第6项、第9项……删去后构成的新数列
中的第3项、第6项、第9项……删去后构成的新数列 中的奇数列与偶数列仍成等比数列,首项分别是
中的奇数列与偶数列仍成等比数列,首项分别是 ,
,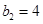 公比均是
公比均是 9分
9分

 … 12分
… 12分
考点:数列的运用
点评:解决的关键是对于数列的分组求和以及等比数列的求和公式得到,属于中档题。

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 ,数列
,数列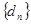 满足
满足 ,数列
,数列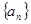 满足
满足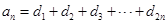 ;数列
;数列 为公比大于
为公比大于 的等比数列,且
的等比数列,且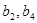 为方程
为方程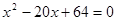 的两个不相等的实根.
的两个不相等的实根.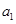 项,第
项,第 项,第
项,第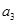 项,……,第
项,……,第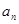 项,……删去后剩余的项按从小到大的顺序排成新数列
项,……删去后剩余的项按从小到大的顺序排成新数列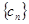 ,求数列
,求数列 项和.
项和.