题目内容
设函数f（x）=lnx+ln（2-x）+ax（a＞0），
（Ⅰ）当a=1时，求f(x)的单调区间；
（Ⅱ）若f（x）在（0，1]上的最大值为
，求a的值。
（Ⅰ）当a=1时，求f(x)的单调区间；
（Ⅱ）若f（x）在（0，1]上的最大值为
，求a的值。 解：函数f(x)的定义域为（0，2），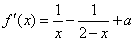
，
（Ⅰ）当a=1时，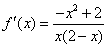
，
所以f（x）的单调递增区间为（0，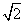
），单调递减区间为（
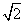，2）；
（Ⅱ）当x∈（0，1]时，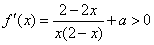
，即f（x）在（0，1]上单调递增，
故f（x）在（0，1]上的最大值为f（1）=a，因此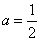
。
练习册系列答案
活力课时同步练习册系列答案
相关题目