题目内容
5、已知P::x2+y2=0(x,y∈R),Q:x≠0或y≠0”则P是-Q的
(填:充分非必要;必要非充分;充要;既非充分又非必要中的一个)
充要
条件.(填:充分非必要;必要非充分;充要;既非充分又非必要中的一个)
分析:根据实数的性质,我们易得到x2+y2=0时,x=0且y=0,这正好是q:x≠0或y≠0的否定,根据充要条件的定义易得到答案.
解答:解:根据实数的性质,x2≥0且y2≥0
故当x2+y2=0时,x=0且y=0
而q:x≠0或y≠0
∴非q:x=0且y=0
故p是非q充要条件
故答案为:充要
故当x2+y2=0时,x=0且y=0
而q:x≠0或y≠0
∴非q:x=0且y=0
故p是非q充要条件
故答案为:充要
点评:本题考查的知识点是充要条件的定义,其中利用实数的性质求出p,及利用复合命题否定的方法求出非q是解答本题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
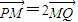 ,点M的轨迹为曲线C.
,点M的轨迹为曲线C.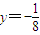 上是否存在点N,使得四边形OANB为矩形,若存在求出N点坐标,若不存在说明理由.
上是否存在点N,使得四边形OANB为矩形,若存在求出N点坐标,若不存在说明理由.