题目内容
已知数列{an}的前n项和Sn= n2+
n2+ n,数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.
n,数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.
(1)求数列{an}、{bn}的通项公式;
(2)设cn= ,数列{cn}的前n项和为Tn,若对任意正整数n,Tn∈[a,b],求b-a的最小值.
,数列{cn}的前n项和为Tn,若对任意正整数n,Tn∈[a,b],求b-a的最小值.
解:(1)因为Sn= n2+
n2+ n,
n,
当n≥2时,an=Sn-Sn-1=n+5,
当n=1时a1=S1=6,满足上式,所以an=n+5,
又因为bn+2-2bn+1+bn=0,所以数列{bn}为等差数列,
由S9=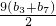 =153,b3=11,故b7=23,
=153,b3=11,故b7=23,
所以公差d= =3,所以bn=b3+(n-3)d=3n+2,
=3,所以bn=b3+(n-3)d=3n+2,
(2)由(1)知cn= =
=
= (
(
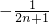 ),
),
所以Tn=c1+c2+…+cn
= [(1-
[(1- )+(
)+( -
- )+…+(
)+…+( -
- )]
)]
= (1-
(1- )=
)= ,
,
又因为Tn+1-Tn= -
- =
=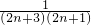 >0,
>0,
所以{Tn}单调递增,故(Tn)min=T1= ,
,
而Tn= <
<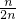 =
= ,故
,故 ≤Tn<
≤Tn< ,
,
所以对任意正整数n,Tn∈[a,b]时,a的最大值为 ,b的最小值为
,b的最小值为 ,故(b-a)min=
,故(b-a)min= -
- =
= .
.
分析:(1)利用已知条件通过an=Sn-Sn-1,求数列{an}的通项公式,利用bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153,求出公差,然后求出{bn}的通项公式;
(2)利用cn= ,求出表达式,通过裂项法直接求解数列{cn}的前n项和为Tn,然后通过数列和的最值求b-a的最小值.
,求出表达式,通过裂项法直接求解数列{cn}的前n项和为Tn,然后通过数列和的最值求b-a的最小值.
点评:本题考查数列递推式,数列的求和,裂项法的应用,数列天通项公式的求法,考查计算能力.
 n2+
n2+ n,
n,当n≥2时,an=Sn-Sn-1=n+5,
当n=1时a1=S1=6,满足上式,所以an=n+5,
又因为bn+2-2bn+1+bn=0,所以数列{bn}为等差数列,
由S9=
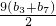 =153,b3=11,故b7=23,
=153,b3=11,故b7=23,所以公差d=
 =3,所以bn=b3+(n-3)d=3n+2,
=3,所以bn=b3+(n-3)d=3n+2,(2)由(1)知cn=
 =
=
=
 (
(
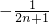 ),
),所以Tn=c1+c2+…+cn
=
 [(1-
[(1- )+(
)+( -
- )+…+(
)+…+( -
- )]
)]=
 (1-
(1- )=
)= ,
,又因为Tn+1-Tn=
 -
- =
=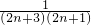 >0,
>0,所以{Tn}单调递增,故(Tn)min=T1=
 ,
,而Tn=
 <
<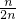 =
= ,故
,故 ≤Tn<
≤Tn< ,
,所以对任意正整数n,Tn∈[a,b]时,a的最大值为
 ,b的最小值为
,b的最小值为 ,故(b-a)min=
,故(b-a)min= -
- =
= .
.分析:(1)利用已知条件通过an=Sn-Sn-1,求数列{an}的通项公式,利用bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153,求出公差,然后求出{bn}的通项公式;
(2)利用cn=
 ,求出表达式,通过裂项法直接求解数列{cn}的前n项和为Tn,然后通过数列和的最值求b-a的最小值.
,求出表达式,通过裂项法直接求解数列{cn}的前n项和为Tn,然后通过数列和的最值求b-a的最小值.点评:本题考查数列递推式,数列的求和,裂项法的应用,数列天通项公式的求法,考查计算能力.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |