Question

已知数列{a_n}的前n项和为S_n,前n项积为T_n,且满足T_n=2^n(1-n).

(1)求a₁;

(2)求证：数列{a_n}为等比数列；

(3)是否存在常数a,使得(S_n+1-a)²=(S_n+2-a)(S_n-a)对n∈N^*都成立？如存在，求出a的值；如不存在，请说明理由.

Answer 1

(1)解：∵T_n=a₁a₂a₃…a_n=2^n(1-n),∴a₁=T₁=1.                                  

(2)证明：当n＞1时，a_n===2^2-2n=()^n-1.                           

又n=1时也适合，∴a_n=()^n-1(n∈N^*).                                        

∴数列{a_n}为等比数列.                                                     

(3)解：∵数列{a_n}为等比数列，

∴S_n=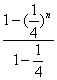=-()ⁿ.                                                

设()ⁿ=b,假设存在满足条件的a值，则有(-b-a)²=［-()²b-a］(-b-a).解之，得a=.

故存在a=满足条件.                                                   

注：利用前三项或等比数列的性质先确定a值，再进行验证亦可.