题目内容

用一块边长为a的正方形白铁皮，在它的四个角各剪去一个小正方形，制成一个无盖的盒子．要使制成的盒子的容积最大，应当剪去多大的小正方形？
设减去的小正方形的边长为x，制成的盒子的容积为V，
则V=x（a-2x）2（0＜x＜
a
2
）
所以V=4x3-4ax2+a2x．
则V′=12x2-8ax+a2，由V′=0，得x=
a
2
（舍）或x=
a
6
．
所以当x=
a
6
，即减去小正方形的面积为
a
6
•
a
6
=
a2
36
时，制成的盒子的容积最大．
练习册系列答案
相关题目
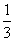已知函数f(x)=x3-ax2+bx（a，b∈R），
（Ⅰ）若f′(0)=f′(2)=1，求函数f(x)的解析式；
（Ⅱ）若b=a+2，且f(x)在区间（0，1）上单调递增，求实数a的取值范围。
函数f（x）=lnx+ln（2-x）+x的单调递增区间为（　　）
A．(0，
2
)		B．(
2
，2)		C．（2，+∞）D．(-
2
，
2
)
已知函数f(x)=
1
3
x3+
1
2
(b-1)x2+cx+d（a，b，c，d∈R）．
（1）若函数f（x）在x=1，x=2处取得极值，求b，c的值；
（2）若函数f（x）在区间（-∞，x1），（x2，+∞）上为增函数，在（x1，x2）上为减函数，且x2-x1＞1，求证：b2＞2（b+2c）；
（3）在（2）的条件下，当t＜x1时，试比较t2+bt+c与x1的大小．
函数y=ln（1+x）-x的单调递增区间为______．
已知函数f（x）是定义在R上的奇函数，f（1）=0，
xf′(x)-f(x)
x2
＞0（x＞0），则不等式f（x）＞0的解集是______．
设f(x)=x3-
3
2
(a+1)x2+3ax+1．
（Ⅰ）若函数f（x）在区间（1，4）内单调递减，求a的取值范围；
（Ⅱ）若函数f（x）在x=a处取得极小值是1，求a的值，并说明在区间（1，4）内函数f（x）的单调性．
已知函数f（x）=ln（x+1）-
x
a(x+1)
．
（1）若函数f（x）在[0，+∞）内为增函数，求正实数a的取值范围．
（2）当a=1时，求f（x）在[-
1
2
，1]上的最大值和最小值；
（3）试利用（1）的结论，证明：对于大于1的任意正整数n，都有
1
2
+
1
3
+
1
4
+…+
1
n
＜lnn．
已知函数f（x）=[ax2-（a+1）x+1]ex，a∈R．
（Ⅰ）若a=1，求函数f（x）的极值；
（Ⅱ）若函数f（x）在区间[0，1]上单调递减，求a的取值范围；
（Ⅲ）在（Ⅰ）的条件下，是否存在区间[m，n]（m＞1）使函数f（x）在[m，n]上的值域也是[m，n]？若存在，求出m，n的值；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网