题目内容
已知△ABC中,角A,B,C的对边分别为a,b,c,BC边上的高为2a,则 的最大值为________.
的最大值为________.

分析:利用三角形的面积公式、余弦定理,化简
 ,再利用辅助角公式,即可求得结论.
,再利用辅助角公式,即可求得结论.解答:∵BC边上的高为2a,
∴
 bcsinA,即a2=2bcsinA
bcsinA,即a2=2bcsinA∵
 =
= =
=
∴
 =
= =2sinA+cosA=
=2sinA+cosA= sin(A+α)(cosα=
sin(A+α)(cosα= ,sinα=
,sinα=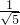 ),
),∴
 的最大值为
的最大值为
故答案为:

点评:本题考查余弦定理及其应用,考查辅助角公式,考查学生的计算能力,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目