题目内容
甲、乙两人练习射击,命中目标的概率分别为 和
和 ,甲、乙两人各射击一次,有下列说法:
,甲、乙两人各射击一次,有下列说法:
①目标恰好被命中一次的概率为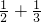 ;
;
②目标恰好被命中两次的概率为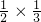 ;
;
③目标被命中的概率为 ;
;
④目标被命中的概率为1- .
.
以上说法正确的序号依次是
- A.②③
- B.①②③
- C.②④
- D.①③
C
分析:①目标恰好被命中一次即是:甲中而乙不中,乙中而甲不中,再依据结论:若A,B相互独立,则P(AB)=P(A)•P(B),即可得到正确结论;
②目标恰好被命中两次表示甲中并且乙中,再依据结论,即可得到正确结论;
③目标被命中包括恰好被命中一次,恰好被命中两次,再依据结论,即可;
④结合题意,目标没命中为目标被命中的对立事件,依据结论:若A,B相互对立,则P(A)=1-P(B),即可得到正确结论.
解答:由题意知,甲、乙两人射击是否命中目标相互独立.
①目标恰好被命中一次的概率为 ,故①错;
,故①错;
②由于目标恰好被命中两次,则两人全部命中,其概率为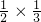 ,故②正确;
,故②正确;
③由于目标被命中包括恰好被命中一次,恰好被命中两次,则其概率为 ,故③错;
,故③错;
④由于目标没命中的概率是 =
= ,则目标被命中的概率为1-
,则目标被命中的概率为1- ,故④正确.
,故④正确.
故答案为C.
点评:本题主要考查相互独立事件的交事件的概率,记住:①若A,B相互独立,则 也相互独立,②若A,B相互独立,则P(AB)=P(A)•P(B).
也相互独立,②若A,B相互独立,则P(AB)=P(A)•P(B).
分析:①目标恰好被命中一次即是:甲中而乙不中,乙中而甲不中,再依据结论:若A,B相互独立,则P(AB)=P(A)•P(B),即可得到正确结论;
②目标恰好被命中两次表示甲中并且乙中,再依据结论,即可得到正确结论;
③目标被命中包括恰好被命中一次,恰好被命中两次,再依据结论,即可;
④结合题意,目标没命中为目标被命中的对立事件,依据结论:若A,B相互对立,则P(A)=1-P(B),即可得到正确结论.
解答:由题意知,甲、乙两人射击是否命中目标相互独立.
①目标恰好被命中一次的概率为
 ,故①错;
,故①错;②由于目标恰好被命中两次,则两人全部命中,其概率为
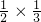 ,故②正确;
,故②正确;③由于目标被命中包括恰好被命中一次,恰好被命中两次,则其概率为
 ,故③错;
,故③错;④由于目标没命中的概率是
 =
= ,则目标被命中的概率为1-
,则目标被命中的概率为1- ,故④正确.
,故④正确.故答案为C.
点评:本题主要考查相互独立事件的交事件的概率,记住:①若A,B相互独立,则
 也相互独立,②若A,B相互独立,则P(AB)=P(A)•P(B).
也相互独立,②若A,B相互独立,则P(AB)=P(A)•P(B). 
练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 和
和 , 甲、乙两人各射击一次,目标被命中的概率为:
, 甲、乙两人各射击一次,目标被命中的概率为: B.
B.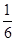 D.
D.
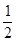 和
和 , 甲、乙两人各射击一次,有下列说法: ①
目标恰好被命中一次的概率为
, 甲、乙两人各射击一次,有下列说法: ①
目标恰好被命中一次的概率为 ;② 目标恰好被命中两次的概率为
;② 目标恰好被命中两次的概率为 ;
③ 目标被命中的概率为
;
③ 目标被命中的概率为 ; ④ 目标被命中的概率为
; ④ 目标被命中的概率为  。以上说法正确的序号依次是
。以上说法正确的序号依次是
 和
和 ,甲、乙两人各射击一次,有下列说法:
,甲、乙两人各射击一次,有下列说法: ;
; ;
;  ;
;  .
. 和
和 ,甲、乙两人各射击一次,有下列说法:
,甲、乙两人各射击一次,有下列说法: ;
; ;
;  ;
;  .
.