题目内容
已知函数f（x）=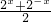
，g（x）=
，
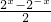（1）计算：[f（1）]2-[g（1）]2；
（2）证明：[f（x）]2-[g（x）]2是定值．
解：（1）[f（1）]2-[g（1）]2=[f（1）+g（1）][f（1）-g（1）]=2×
=．
（2）：[f（x）]2-[g（x）]2=[f（x）+g（x）][f（x）-g（x）]
=
=2x×2-x=1为定值．
∴本题得证．
分析：（1）直接代入计算即可：[f（1）]2-[g（1）]2=[f（1）+g（1）][f（1）-g（1）]；
（2）先利用平方差公式化得：[f（x）]2-[g（x）]2=[f（x）+g（x）][f（x）-g（x）]，再将条件整体代入即可．
点评：本小题主要考查函数的值、函数恒成立问题等基础知识，考查运算求解能力，解答关键是利用整体思想代入求解，属于基础题．
=．（2）：[f（x）]2-[g（x）]2=[f（x）+g（x）][f（x）-g（x）]
=
=2x×2-x=1为定值．
∴本题得证．
分析：（1）直接代入计算即可：[f（1）]2-[g（1）]2=[f（1）+g（1）][f（1）-g（1）]；
（2）先利用平方差公式化得：[f（x）]2-[g（x）]2=[f（x）+g（x）][f（x）-g（x）]，再将条件整体代入即可．
点评：本小题主要考查函数的值、函数恒成立问题等基础知识，考查运算求解能力，解答关键是利用整体思想代入求解，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|