题目内容
已知两条直线 ,求满足下列条件的
,求满足下列条件的 的值:
的值:
(Ⅰ)l1⊥l2,且l1过点(-3,-1);
(Ⅱ)l1//l2,且坐标原点到这两条直线的距离相等.
(Ⅰ)由已知可得l2的斜率必存在,∴
若 ∵l1⊥l2,直线l1的斜率
∵l1⊥l2,直线l1的斜率 必不存在,即b=0.
必不存在,即b=0.
又∵l1过点(-3,-1),∴ (不合题意),∴此种情况不存在,即
(不合题意),∴此种情况不存在,即
若 ,即
,即 、
、 都存在,
都存在, ⊥
⊥ ,
, ……①
……①
又∵l1过点(-3,-1), ……②
……②
由①②联立,解得a=2,b=2.
(Ⅱ)∵l2的斜率存在,且l1//l2,∴直线l1的斜率存在,∴ ……③
……③
又∵坐标原点到这两条直线的距离相等,且l1//l2,∴l1、l2在y轴上的截距互为相反数,
即 ……④
……④
则联立③④解得 ∴a,b的值为2和-2,或
∴a,b的值为2和-2,或

练习册系列答案
相关题目
 =(1,5,-2),
=(1,5,-2), =(3,1,z),若
=(3,1,z),若 =(x-1,y,-3),且BP⊥平面ABC,则实数x,y,z分别为 ( )
=(x-1,y,-3),且BP⊥平面ABC,则实数x,y,z分别为 ( )  ,-
,- ,4 B.
,4 B. ,-
,- 设
设  表示
表示 中的较大值,
中的较大值, 表示
表示 的最小值为
的最小值为
 的最大值为
的最大值为 ,则
,则 ( )
( ) (B)
(B) (C)16 (D)-16
(C)16 (D)-16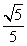 的点的集合是( )
的点的集合是( ) 0)共线,则
0)共线,则 的值等于 .
的值等于 .  的定义域为 ( )
的定义域为 ( ) B.
B. C.
C. D.
D.
 的二次方程
的二次方程 的两个实数根互为倒数,则
的两个实数根互为倒数,则 = _____.
= _____. B.1∶3 C.1∶3
B.1∶3 C.1∶3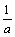 ) ②1oga(1+o)>loga(1+
) ②1oga(1+o)>loga(1+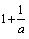 ④a1+a>a
④a1+a>a