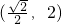题目内容
已知方程:x2+ax+2b=0(a∈R,b∈R),其一根在区间(0,1)内.另一根在区间(1,2)内,则z=(a+3)2+b2的取值范围为( )
A、(
| ||||
B、(
| ||||
| C、(1,2) | ||||
| D、(1,4) |
分析:令f(x)=x2+ax+2b,根据题意可知f(0)>0,f(1)<0,f(2)>0,进而求得b>0,a+2b+1<0,a+b+2>0,画出可行域,进而分别求得z的最大和最小值,答案可得.
解答:解:设f(x)=x2+ax+2b由函数图象可知:f(0)>0,
f(1)<0,f(2)>0三者同时成立,
求解得b>0,a+2b+1<0,2a+2b+4>0,
由线性规划的知识画出可行域:以a为横轴,b纵轴,
再以z=(a+3)2+b2为目标,几何意义即为区域内的点到(-3,0)的距离的平方
当a=-1,b=0时,zmax=4,当点到直线a+b+2=0的距离为
,zmin=
由题目,不能取边界,
∴z∈(
,4)
故选B

f(1)<0,f(2)>0三者同时成立,
求解得b>0,a+2b+1<0,2a+2b+4>0,
由线性规划的知识画出可行域:以a为横轴,b纵轴,
再以z=(a+3)2+b2为目标,几何意义即为区域内的点到(-3,0)的距离的平方
当a=-1,b=0时,zmax=4,当点到直线a+b+2=0的距离为
| ||
| 2 |
| 1 |
| 2 |
由题目,不能取边界,
∴z∈(
| 1 |
| 2 |
故选B
点评:本题主要考查了一元二次方程根据的分布,以及线性规划的基本知识.考查了学生对基础知识的综合运用.

练习册系列答案
相关题目