Question

【题目】若对于任意的x∈[﹣1，0]，关于x的不等式3x2+2ax+b≤0恒成立，则a2+b2﹣2的最小值为（ ）
A.
B.
C.
D.

Answer 1

【答案】A
【解析】解：对于任意的x∈[﹣1，0]，关于x的不等式3x2+2ax+b≤0恒成立，
令f（x）=3x2+2ax+b，
即f（x）≤0恒成立，
满足： ，
解得：
该不等式表示的平面区域如图中阴影部分所示，
设z=a2+b2﹣2，a2+b2=2+z；
∴该方程表示以原点为圆心，半径为 的圆；
原点到直线﹣2a+b+3=0的距离等于最小的半径；
∴该圆的半径 ；
解得；
∴a2+b2﹣2的最小值为 ．
故选：A．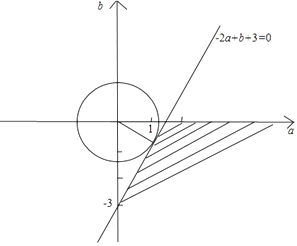

【考点精析】解答此题的关键在于理解二次函数的性质的相关知识，掌握当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减．