题目内容
已知定义域为R的函数f(x)满足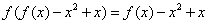 。
。
(1)若f(2)=3,求f(1);又若f(0)=a,求f(a);
(2)设有且仅有一个实数x0,使得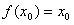 ,求函数f(x)的表达式。
,求函数f(x)的表达式。
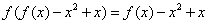 。
。(1)若f(2)=3,求f(1);又若f(0)=a,求f(a);
(2)设有且仅有一个实数x0,使得
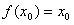 ,求函数f(x)的表达式。
,求函数f(x)的表达式。 解:(1)因为对任意的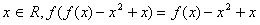 ,
,
所以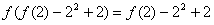 。
。
又由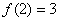 ,得
,得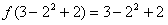 ,即
,即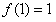 。
。
若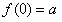 ,则
,则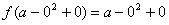 ,即
,即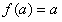 。
。
(2)因为对任意的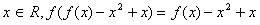 ,
,
又因为有且仅有一个实数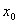 ,使得
,使得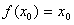 ,
,
所以对任意的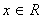 ,有
,有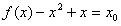 ,
,
在上式中令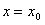 ,有
,有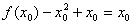 ,
,
又因为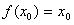 ,所以
,所以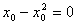 ,故
,故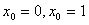 。
。
①若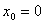 ,则
,则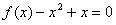 ,即
,即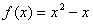 ,
,
但方程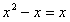 有两个不同的实数根,与题设条件不符,故
有两个不同的实数根,与题设条件不符,故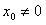 。
。
②若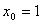 ,则
,则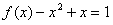 ,即
,即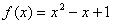 ,易验证该函数满足题设条件。
,易验证该函数满足题设条件。
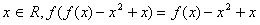 ,
,所以
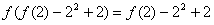 。
。又由
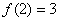 ,得
,得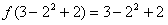 ,即
,即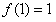 。
。若
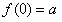 ,则
,则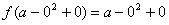 ,即
,即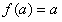 。
。 (2)因为对任意的
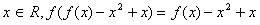 ,
,又因为有且仅有一个实数
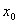 ,使得
,使得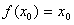 ,
,所以对任意的
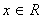 ,有
,有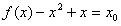 ,
,在上式中令
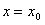 ,有
,有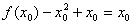 ,
,又因为
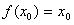 ,所以
,所以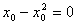 ,故
,故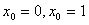 。
。①若
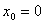 ,则
,则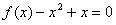 ,即
,即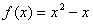 ,
,但方程
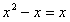 有两个不同的实数根,与题设条件不符,故
有两个不同的实数根,与题设条件不符,故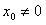 。
。②若
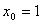 ,则
,则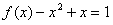 ,即
,即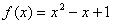 ,易验证该函数满足题设条件。
,易验证该函数满足题设条件。 
练习册系列答案
相关题目