题目内容
设函数f(x)=x2+(m-1)x+1在区间[0,2]上有两个零点,则实数m的取值范围是 .
【答案】分析:当f(x)在[0,2]上有两个零点时,即方程x2+(m-1)x+1=0在区间[0,2]上有两个不相等的实根,由此构造关于m的不等式组,解不等式组可求出m的取值范围.
解答:解:当f(x)在[0,2]上有两个零点时,
此时方程x2+(m-1)x+1=0在区间[0,2]上有两个不相等的实根,
则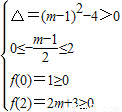 ,
,
解得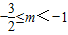 ,
,
实数m的取值范围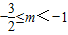
故答案为: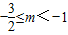
点评:本题考查二次函数与方程之间的关系,二次函数在给定区间上的零点问题,要注意函数图象与x轴相切的情况,属于中档题.
解答:解:当f(x)在[0,2]上有两个零点时,
此时方程x2+(m-1)x+1=0在区间[0,2]上有两个不相等的实根,
则
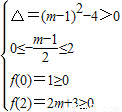 ,
,解得
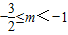 ,
,实数m的取值范围
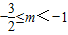
故答案为:
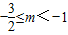
点评:本题考查二次函数与方程之间的关系,二次函数在给定区间上的零点问题,要注意函数图象与x轴相切的情况,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目