题目内容
直线L:y=k(x+3)与圆O:x2+y2=4交于A、B两点,则当△AOB的面积最大时,k=
±
| ||
| 7 |
±
.
| ||
| 7 |
分析:由圆的方程找出圆心O坐标和半径r,同时把直线l的方程整理为一般式方程,然后利用点到直线的距离公式表示出圆心O到直线l的距离d,即为圆O中弦AB的弦心距,根据垂径定理得到垂足为弦AB的中点,由圆的半径,弦心距及弦的一半构成的直角三角形,利用勾股定理表示出弦AB的长度,然后利用三角形的面积公式底乘以高除以2,用含有d的式子表示出三角形ABC的面积,并利用基本不等式
≤
求出面积的最大值,以及面积取得最大值时d的值,从而列出关于k的方程,求出方程的解即可得到面积最大时k的值.
| ab |
| a+b |
| 2 |
解答:解:由圆O:x2+y2=4,得到圆心坐标为(0,0),半径r=2,
把直线l的方程为y=k(x+3),整理为一般式方程得:kx-y+3k=0,
∴圆心O(0,0)到直线AB的距离d=
,(9分)
弦AB的长度|AB|=2
=2
,
∴S△ABC=
|AB|d=d
=
≤
=2,(11分)
当且仅当d2=2时取等号,S△ABC取得最大值,最大值为2,
此时
=2,解得k=±
.
故答案为:±
把直线l的方程为y=k(x+3),整理为一般式方程得:kx-y+3k=0,
∴圆心O(0,0)到直线AB的距离d=
| 3|k| | ||
|
弦AB的长度|AB|=2
| r2-d2 |
| 4 -d2 |
∴S△ABC=
| 1 |
| 2 |
| 4-d2 |
| d2(4-d2) |
| d2+(4-d2) |
| 2 |
当且仅当d2=2时取等号,S△ABC取得最大值,最大值为2,
此时
| 9k2 |
| k2+1 |
| ||
| 7 |
故答案为:±
| ||
| 7 |
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,直线的一般式方程,点到直线的距离公式,垂径定理,勾股定理,以及基本不等式的应用,当直线与圆相交时,常常由弦长的一半,弦心距,以及圆的半径构造直角三角形,利用勾股定理来解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
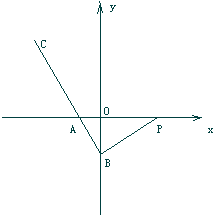 如图,已知直角三角形PAB的直角顶点为B,点P的坐标为(3,0),点B在y轴上,点A在x轴的负半轴上,在BA的延长线上取一点C,使
如图,已知直角三角形PAB的直角顶点为B,点P的坐标为(3,0),点B在y轴上,点A在x轴的负半轴上,在BA的延长线上取一点C,使