题目内容
在数列![]() 与
与![]() 中,
中,![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() ,
,![]() 为
为![]() 与
与![]() 的等比中项,
的等比中项,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求数列![]() 与
与![]() 的通项公式;
的通项公式;
(Ⅲ)设.![]()
![]() 证明:
证明:![]() .
.
(Ⅰ)解:由题设有![]() ,
,![]() ,解得
,解得![]() .由题设又有
.由题设又有![]() ,
,![]() ,解得
,解得![]() .
.
(Ⅱ)解法一:由题设![]() ,
,![]() ,
,![]() ,及
,及![]() ,
,![]() ,进一步可得
,进一步可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
猜想![]() ,
,![]() ,
,![]() .
.
先证![]() ,
,![]() .
.
当![]() 时,
时,![]() ,等式成立.当
,等式成立.当![]() 时用数学归纳法证明如下:
时用数学归纳法证明如下:
(1)当![]() 时,
时,![]() ,等式成立.
,等式成立.
(2)假设![]() 时等式成立,即
时等式成立,即![]() ,
,![]() .
.
![]() 由题设,
由题设,![]()
![]()
①的两边分别减去②的两边,整理得![]() ,从而
,从而
![]() .
.
这就是说,当![]() 时等式也成立.根据(1)和(2)可知,等式
时等式也成立.根据(1)和(2)可知,等式![]() 对任何的
对任何的![]() 成立.
成立.
综上所述,等式![]() 对任何的
对任何的![]() 都成立
都成立
再用数学归纳法证明![]() ,
,![]() .
.
(1)当![]() 时,
时,![]() ,等式成立.
,等式成立.
(2)假设当![]() 时等式成立,即
时等式成立,即![]() ,那么
,那么
![]() .
.
这就是说,当![]() 时等式也成立.根据(1)和(2)可知,等式
时等式也成立.根据(1)和(2)可知,等式![]() 对任何的
对任何的![]() 都成立.
都成立.
![]() 解法二:由题设
解法二:由题设![]()
![]()
①的两边分别减去②的两边,整理得![]() ,
,![]() .所以
.所以
![]() ,
,
![]() ,
,
……
![]() ,
,![]() .
.
将以上各式左右两端分别相乘,得![]() ,
,
由(Ⅰ)并化简得![]() ,
,![]() .
.
上式对![]() 也成立.
也成立.
由题设有![]() ,所以
,所以![]() ,
,
即![]() ,
,![]() .
.
令![]() ,则
,则![]() ,即
,即![]() .
.
由![]() 得
得![]() ,
,![]() .所以
.所以![]() ,
,
即![]() ,
,![]() .
.
解法三:由题设有![]() ,
,![]() ,所以
,所以
![]() ,
,
![]() ,
,
……
![]() ,
,![]() .
.
将以上各式左右两端分别相乘,
得![]() ,化简得
,化简得
![]() ,
,![]() .
.
由(Ⅰ),上式对![]() 也成立.所以
也成立.所以![]() ,
,![]() .
.
上式对![]() 时也成立.
时也成立.
以下同解法二,可得![]() ,
,![]() .
.
(Ⅲ)证明:![]() .
.
当![]() ,
,![]() 时,
时,
![]() .
.
注意到![]() ,故
,故
![]()
![]() .
.
当![]() ,
,![]() 时,
时,![]()
当![]() ,
,![]() 时,
时,
![]() .
.
当![]() ,
,![]() 时,
时,
![]() .
.
所以 .
.
从而![]() 时,有
时,有
总之,当![]() 时有
时有![]() ,即
,即![]() .
.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
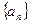 与
与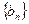 中,
中, ,数列
,数列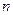 项和
项和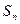 满足
满足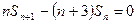 ,
, 为
为 与
与 的等比中项,
的等比中项,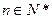 .
. 的值;
的值;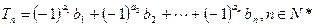 .证明
.证明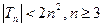 .
. 与
与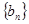 中,
中,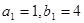 ,数列
,数列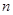 项和
项和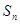 满足
满足 ,
,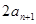 为
为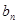 与
与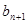 的等比中项,
的等比中项, .
.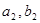 的值;
的值;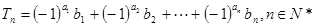 .证明
.证明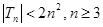 .
.