题目内容
(本小题满分12分)
设函数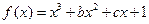 的单调减区间是(1,2)
的单调减区间是(1,2)
⑴求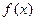 的解析式;
的解析式;
⑵若对任意的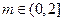 ,关于
,关于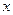 的不等式
的不等式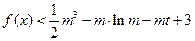 在
在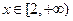 时有解,求实数
时有解,求实数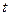 的取值范围.
的取值范围.
解:⑴ .
.
∵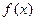 的单调减区间是(1,2),∴
的单调减区间是(1,2),∴ ,………3分
,………3分
∴
∴ . ………5分
. ………5分
⑵由⑴得 ,[来源:Z。xx。k.Com]
,[来源:Z。xx。k.Com]
当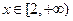 时,
时, ≥0,∴
≥0,∴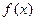 在
在 单调递增,
单调递增,
∴
 .
.
要使关于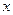 的不等式
的不等式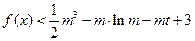 在
在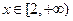 时有解,
时有解,
即
 , ………7分
, ………7分
即 对任意
对任意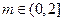 恒成立,
恒成立,
只需 在
在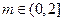 恒
恒 成立.
成立.
设 ,
,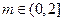 ,则
,则 . ………9分
. ………9分 ,
,
当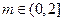 时,
时, 在
在 上递减,在
上递减,在 上递增,:学,科,网]
上递增,:学,科,网]
∴ .
.
∴ . ………12分
. ………12分
解析

练习册系列答案
相关题目
 为实数,
为实数, ,
,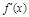 为
为 的导函数.
的导函数. ,求
,求 上的最大值和最小值;
上的最大值和最小值; 和
和 上均单调递增,求
上均单调递增,求 .(e是自然对数的底数)
.(e是自然对数的底数) 在
在 上是否是单调函数,并写出
上是否是单调函数,并写出
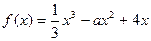
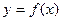 在点
在点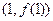 处的切线的倾斜角为
处的切线的倾斜角为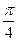 ,求实数
,求实数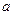 的值;
的值;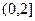 上单调递增,求实数实数
上单调递增,求实数实数
 时,求函数
时,求函数 的单调区间;
的单调区间; 的图像在点
的图像在点 处的切线的倾斜角为
处的切线的倾斜角为 ,问:
,问: 在什么范围取值时,函数
在什么范围取值时,函数 在区间
在区间 上总存在极值?
上总存在极值? .
. 在
在 上为增函数,求实数a的取值范围;
上为增函数,求实数a的取值范围; 时,设
时,设 ,求
,求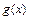 在
在 上的最大值和最小值.
上的最大值和最小值.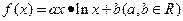 ,在点
,在点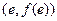 处的切
处的切 线方程是
线方程是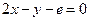 (e为自然对数的底)。
(e为自然对数的底)。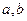 的值及
的值及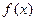 的解析式;
的解析式;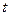 是正数,设
是正数,设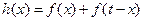 ,求
,求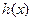 的最小值;
的最小值; 于x的不等式
于x的不等式 对一切
对一切 恒成立,求实数
恒成立,求实数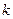 的取值范围
的取值范围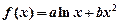 在点
在点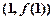 处的切线方程为
处的切线方程为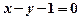 .
.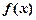 的表达式;
的表达式; 若
若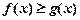 恒成立,则称
恒成立,则称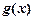 的一个“上界函数”,如果函数
的一个“上界函数”,如果函数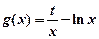 (
(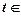 R)的一个“上界函数”,求t的取值范围;
R)的一个“上界函数”,求t的取值范围;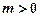 时,讨论
时,讨论 在区间(0,2)上极值点的个数.
在区间(0,2)上极值点的个数. 3,6],不等式f(x)≤1在x∈[-2,2]上恒成立,求m的取值范围.
3,6],不等式f(x)≤1在x∈[-2,2]上恒成立,求m的取值范围.