题目内容
在
中，角A、B、C的对边分别为a、b、c，且角A、B、C成等差教列．
(I)若
，求边c的值；
(II)设
，求
的最大值．
【答案】
（Ⅰ）
.（Ⅱ）
.
【解析】
试题分析：（Ⅰ）由角
成等差数列，及
，首先得到
.
进一步应用余弦定理即得所求.
（Ⅱ）根据
，可化简得到
根据
,即可得到
时，
有最大值.
试题解析：（Ⅰ）因为角成等差数列，所以
，
因为，所以. 2分
因为
，
，
,
所以
.
所以或
(舍去)．
6分
（Ⅱ）因为，
所以
9分
因为
，所以,
所以当
，即时，有最大值.
12分
考点：等差数列，和差倍半的三角函数，，三角函数的性质，余弦定理的应用.
练习册系列答案
相关题目
中，角A、B、C的对边分别为
、
、
．且
．
的值；
，
求
的最大值．
，其中向量
，
，
.在
中，角A、B、C的对边分别为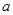
，
，
.
的取值范围及此时函数
的值域；
，边
，求
中，角A，B，C的对边分别为
，AH为BC边上的高，
；②
；
，则
。
中，角A，B，C的对边分别为
，
，
，已知A=
，
，
，则
D．
中，角A、B、C的对边分别为
、
、
，
，C
，求边