题目内容
设M={平面内的点（a，b）}，N={f(x)|f(x)=acos2x+bsin2x}，给出M到N的映射f：（a，b）→f(x)=acos2x+bsin2x，若点（1，
）的像f(x)的图象可以由曲线y=2sin2x按向量m平移得到，则向量m的坐标为
）的像f(x)的图象可以由曲线y=2sin2x按向量m平移得到，则向量m的坐标为 [ ]
A．（
，0）
B．（-
，0）
C．（-
，0）
D．（
，0）
，0） B．（-
，0）C．（-
，0）D．（
，0） B
练习册系列答案
相关题目
的像f（x）的图象可以由曲线y=2sin2x按向量
平移得到，则向量
的坐标为（ ）
的像f（x）的图象可以由曲线y=2sin2x按向量
平移得到，则向量
的坐标为（ ）
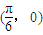
的像f（x）的最小正周期是（ ）
