题目内容
已知实数x，y满足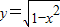
，则x+y的最小值是（ ）A．-1
B．1
C．
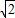
D．
【答案】分析：根据题意设x=cosα，可得y=sinα，其中α∈[0，π]．从而得出x+y=cosα+sinα=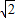
sin（
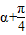），利用正弦函数的图象与性质，结合α的范围得到α=π时，x+y的最小值等于-1．
解答：解：设x=cosα，则y=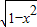
=sinα（α∈[0，π]）
因此x+y=cosα+sinα=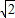
sin（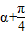
）
∵
∈[
，
]
∴
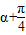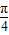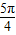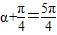时，即α=π时，x+y的最小值等于-1
故选：A
点评：本题给出函数关系式，求式子x+y的最小值．着重考查了三角换元的方法解决函数求最值的知识点，属于中档题．
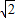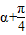sin（），利用正弦函数的图象与性质，结合α的范围得到α=π时，x+y的最小值等于-1．解答：解：设x=cosα，则y=
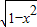=sinα（α∈[0，π]）因此x+y=cosα+sinα=
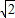sin（）∵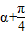
∈[，]∴
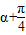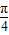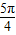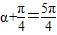时，即α=π时，x+y的最小值等于-1故选：A
点评：本题给出函数关系式，求式子x+y的最小值．着重考查了三角换元的方法解决函数求最值的知识点，属于中档题．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目