Question

已知动点P与双曲线的两个焦点F₁，F₂的距离之和为定值，

且cos∠F₁PF₂的最小值为－.

（1）求动点P的轨迹方程；（6分）

（2）是否存在直线l与P点轨迹交于不同的两点M、N，且线段MN恰被直线

平分？若存在，求出直线l的斜率k的取值范围，若不存在说明理由.

 

Answer 1

【答案】

解: (1)∵，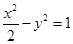

∴c＝.设|PF₁|＋|PF₂|＝2a(常数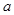＞0)，------2分

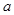2＞2c＝2，∴＞

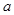由余弦定理有cos∠F₁PF₂＝

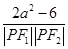＝＝－1

∵|PF₁||PF₂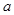|≤()²＝²，

∴当且仅当|PF₁|＝|PF₂|时，|PF₁||PF₂|取得最大值a².

此时cos∠F₁PF₂取得最小值-1，----------4分

由题意－1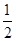＝－，解得a²＝4，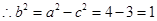

∴P点的轨迹方程为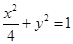------------6分

（2）由（1）知p点轨迹为椭圆，显然直线l的斜率k存在，

设l的直线方程为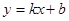   ------------7分

  由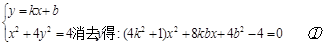

设l与椭圆交于不同两点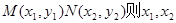

为方程①的两个不同根

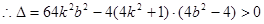
解得：  ②------------9分

又 且MN被直线x=－1平分

  

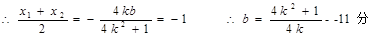
代入②解不等式 ，解得

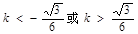
  ∴存在直线l满足条件，l的斜率k的范围是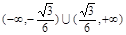

------------12分

【解析】略