题目内容
【题目】已知二次函数f（x）满足f（-x-1）=f（x-1），其图象过点（0，1），且与x轴有唯一交点。
（1）求f（x）的解析式；
（2）设函数g（x）=f（x）-（2+a）x，求g（x）在[1，2]上的最小值h（a）。
【答案】（1）
；（2）
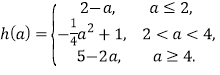
【解析】试题分析：（1）利用待定系数法设
，依题意过点可得
，由对称轴可得
，由图象与
轴有唯一交点零点可得
，解出方程组可得函数解析式；（2）结合（1）可得函数
的对称轴为
，利用分类讨论思想分为
，
和
三种情形，得到函数单调性，故可得其最值.
试题解析：（1）设二次函数
的解析式为，因为
，所以函数对称轴为
。
因为图象过点
，所以，因为函数的图象与轴有唯一交点，所以，所以
，
，，所以.
（2）
，函数图象对称轴为，且开口向上，
当时，即
时，函数在
上单调递增，所以
；
当时，即
时，在
上单调递减，在
上单调递增，所以
；当即
时，函数在上单调递减，
所以
，所以h（a）=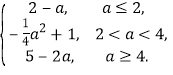
练习册系列答案
应用题作业本系列答案
相关题目
