题目内容

设数列{a_n}的前n项和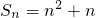 $数学公式$ ，则a₇的值为________．

14
分析：根据数列的前n项和与第n项之间的关系求出通项公式，根据通项公式求出a₇的值．
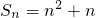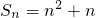解答：数列{a_n}的前n项和 $\text{[math]}$ ，则有a₁=s₁=2，
当n≥2时，a_n=s_n-s_n-1=（n²+n）-[（n-1）²+（n-1）]=2n，
综上可得，a_n=2n，故 a₇的值为2×7=14，
故答案为 14．
点评：本题主要考查等差数列的定义和性质，数列的前n项和与第n项之间的关系，属于中档题．

练习册系列答案

智慧大考卷系列答案

导学案广东经济出版社系列答案

优佳好书系讲与练系列答案

课课练与单元检测系列答案

高中基础训练山东教育出版社系列答案

名校学案名校小状元系列答案

全优课堂满分备考系列答案

专题王系列答案

学考联通寒假作业冲刺中考长江出版社系列答案

必胜课课课达标系列答案

相关题目

设数列{a_n}的前n项的和为S_n，且S_n=3ⁿ+1．
（1）求数列{a_n}的通项公式；
（2）设b_n=a_n（2n-1），求数列{b_n}的前n项的和．

设数列a_n的前n项的和为S_n，a1=

，Sn=2an+1-3．
（1）求a₂，a₃；
（2）求数列a_n的通项公式；
（3）设bn=(2log

an+1)•an，求数列b_n的前n项的和T_n．

设数列{a_n}的前n项和S_n=2a_n+

，n∈N^*．
（Ⅰ）求a_n和a_n-1的关系式；
（Ⅱ）求数列{a_n}的通项公式；
（Ⅲ）证明：

所表示的平面区域为D_n，若D_n内的整点（整点即横坐标和纵坐标均为整数的点）个数为a_n（n∈N^*）
（1）写出a_n+1与a_n的关系（只需给出结果，不需要过程），
（2）求数列{a_n}的通项公式；
（3）设数列a_n的前n项和为S_n且Tn=

，若对一切的正整数n，总有T_n≤m成立，求m的范围．

（2013•郑州一模）设数列{a_n}的前n项和Sn=2n-1，则

的值为（　　）