题目内容
设二次函数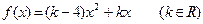 ,对任意实数
,对任意实数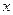 ,有
,有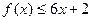 恒成立;数列
恒成立;数列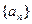 满足
满足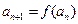 .
.
(1)求函数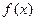 的解析式和值域;
的解析式和值域;
(2)试写出一个区间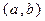 ,使得当
,使得当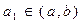 时,数列
时,数列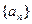 在这个区间上是递增数列,并说明理由;
在这个区间上是递增数列,并说明理由;
(3)已知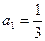 ,是否存在非零整数
,是否存在非零整数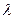 ,使得对任意
,使得对任意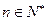 ,都有
,都有
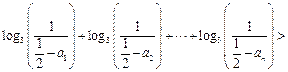
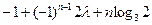 恒成立,若存在,
恒成立,若存在,
求之;若不存在,说明理由.
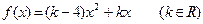 ,对任意实数
,对任意实数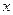 ,有
,有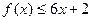 恒成立;数列
恒成立;数列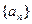 满足
满足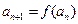 .
.(1)求函数
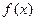 的解析式和值域;
的解析式和值域;(2)试写出一个区间
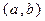 ,使得当
,使得当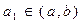 时,数列
时,数列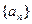 在这个区间上是递增数列,并说明理由;
在这个区间上是递增数列,并说明理由;(3)已知
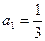 ,是否存在非零整数
,是否存在非零整数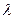 ,使得对任意
,使得对任意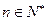 ,都有
,都有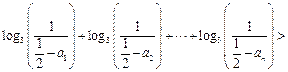
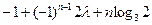 恒成立,若存在,
恒成立,若存在,求之;若不存在,说明理由.
解:(1)由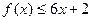 恒成立等价于
恒成立等价于 恒成立,…1分
恒成立,…1分
从而得: ,化简得
,化简得 ,从而得
,从而得 ,
,
所以 ,………3分
,………3分
其值域为 .…………………4分
.…………………4分
(2)解:当 时,数列
时,数列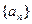 在这个区间上是递增数列,证明如下:
在这个区间上是递增数列,证明如下:
设 ,则
,则 ,
,
所以对一切 ,均有
,均有 ;………………7分
;………………7分


从而得 ,即
,即 ,所以数列
,所以数列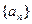 在区间
在区间 上是递增数列…10分
上是递增数列…10分
注:本题的区间也可以是 、
、 、
、 等无穷多个.
等无穷多个.
另解:若数列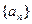 在某个区间上是递增数列,则
在某个区间上是递增数列,则
即
 …7分
…7分
又当 时,
时, ,
,
∴对一切 ,均有
,均有 且
且 ,
,
∴数列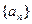 在区间
在区间 上是递增数列.…………………………10分
上是递增数列.…………………………10分
(3)(文科)由(2)知 ,从而
,从而 ;
;
 ,
,
即 ; ………12分
; ………12分
令 ,则有
,则有 且
且 ;
;
从而有 ,可得
,可得 ,
,
∴数列 是以
是以 为首项,公比为
为首项,公比为 的等比数列,………14分
的等比数列,………14分
从而得 ,即
,即 ,
,
∴ ,
,
∴ ,∴
,∴ , …16分
, …16分
∴,
 . ………………………18分
. ………………………18分
(3)(理科)由(2)知 ,从而
,从而 ;
;
 ,
,
即 ;………12分
;………12分
令 ,则有
,则有 且
且 ;
;
从而有 ,可得
,可得 ,所以数列
,所以数列 是
是 为首项,公比为
为首项,公比为 的等比数列,…………………14分
的等比数列,…………………14分
从而得 ,即
,即 ,
,
所以 ,
,
所以 ,所以
,所以 ,
,
所以,
 .………………………16分
.………………………16分
即

 ,所以,
,所以, 恒成立
恒成立
(1)当n为奇数时,即 恒成立,当且仅当
恒成立,当且仅当 时,
时, 有最小值
有最小值 为。
为。
(2)当n为偶数时,即 恒成立,当且仅当
恒成立,当且仅当 时,有最大值
时,有最大值 为。
为。
所以,对任意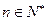 ,有
,有 。又
。又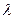 非零整数,
非零整数, …………18分
…………18分
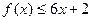 恒成立等价于
恒成立等价于 恒成立,…1分
恒成立,…1分从而得:
 ,化简得
,化简得 ,从而得
,从而得 ,
,所以
 ,………3分
,………3分其值域为
 .…………………4分
.…………………4分(2)解:当
 时,数列
时,数列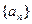 在这个区间上是递增数列,证明如下:
在这个区间上是递增数列,证明如下:设
 ,则
,则 ,
,所以对一切
 ,均有
,均有 ;………………7分
;………………7分

从而得
 ,即
,即 ,所以数列
,所以数列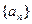 在区间
在区间 上是递增数列…10分
上是递增数列…10分注:本题的区间也可以是
 、
、 、
、 等无穷多个.
等无穷多个.另解:若数列
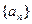 在某个区间上是递增数列,则
在某个区间上是递增数列,则
即

 …7分
…7分又当
 时,
时, ,
,∴对一切
 ,均有
,均有 且
且 ,
,∴数列
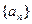 在区间
在区间 上是递增数列.…………………………10分
上是递增数列.…………………………10分(3)(文科)由(2)知
 ,从而
,从而 ;
; ,
,即
 ; ………12分
; ………12分令
 ,则有
,则有 且
且 ;
;从而有
 ,可得
,可得 ,
,∴数列
 是以
是以 为首项,公比为
为首项,公比为 的等比数列,………14分
的等比数列,………14分从而得
 ,即
,即 ,
,∴
 ,
,∴
 ,∴
,∴ , …16分
, …16分∴,

 . ………………………18分
. ………………………18分(3)(理科)由(2)知
 ,从而
,从而 ;
; ,
,即
 ;………12分
;………12分令
 ,则有
,则有 且
且 ;
;从而有
 ,可得
,可得 ,所以数列
,所以数列 是
是 为首项,公比为
为首项,公比为 的等比数列,…………………14分
的等比数列,…………………14分从而得
 ,即
,即 ,
,所以
 ,
,所以
 ,所以
,所以 ,
,所以,

 .………………………16分
.………………………16分即


 ,所以,
,所以, 恒成立
恒成立(1)当n为奇数时,即
 恒成立,当且仅当
恒成立,当且仅当 时,
时, 有最小值
有最小值 为。
为。
(2)当n为偶数时,即
 恒成立,当且仅当
恒成立,当且仅当 时,有最大值
时,有最大值 为。
为。
所以,对任意
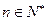 ,有
,有 。又
。又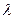 非零整数,
非零整数, …………18分
…………18分略

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
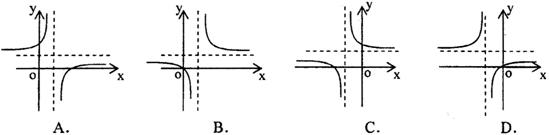
 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, ,则函数
,则函数 的大致图像为
的大致图像为
 的图像,对函数y来说下列判定成立的是
的图像,对函数y来说下列判定成立的是
 B.在
B.在 上是增函数C.
上是增函数C. 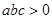 D.图象关于
D.图象关于 对称
对称 的图象与函数g(x)的
的图象与函数g(x)的 图象关于直线
图象关于直线 对称,令
对称,令 则关于函数
则关于函数 有下列命题 ( )
有下列命题 ( ) 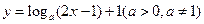 的图象过定点 .
的图象过定点 .

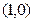 的是( )
的是( )



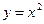
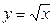 的图像是( ▲ )
的图像是( ▲ )
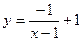 的图象是下列图象中的 ( )
的图象是下列图象中的 ( )