题目内容
如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD为直角梯形,AD∥BC,AD⊥CD.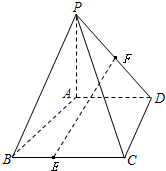 (Ⅰ)求证:CD⊥PD;
(Ⅰ)求证:CD⊥PD;(Ⅱ)若AD=2,BC=3,F为PD中点,BE=
| 1 | 3 |
分析:(I)根据已知中PA⊥底面ABCD,四边形ABCD为直角梯形,AD∥BC,AD⊥C,结合线面垂直的定义及线面垂直的判定定理,我们易得到结论;
(II)根据已知中AD=2,BC=3,F为PD中点,BE=
BC,取PA的中点G,连接EG,FG,AE,BG,我们易得到EF∥BG,结合线面平行的判定定理,即可得到答案.
(II)根据已知中AD=2,BC=3,F为PD中点,BE=
| 1 |
| 3 |
解答: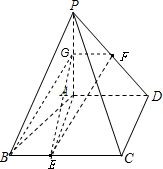 解:(I)∵PA⊥底面ABCD,
解:(I)∵PA⊥底面ABCD,
∴PA⊥CD,
又∵AD⊥CD,AD∩PA=A
∴CD⊥平面PAD
又由PD?平面PAD
∴CD⊥PD;
(II)取PA的中点G,连接EG,FG,AE,BG
则GF=
AD=1,且GF∥AD
BE=
BC=1,且BE∥AD
故BE=GF,且BE∥GF
故四边形BEGF为平行四边形
则EF∥BG
又∵EF?平面PAB,BG?平面PAB
故EF∥平面PAB
 解:(I)∵PA⊥底面ABCD,
解:(I)∵PA⊥底面ABCD,∴PA⊥CD,
又∵AD⊥CD,AD∩PA=A
∴CD⊥平面PAD
又由PD?平面PAD
∴CD⊥PD;
(II)取PA的中点G,连接EG,FG,AE,BG
则GF=
| 1 |
| 2 |
BE=
| 1 |
| 3 |
故BE=GF,且BE∥GF
故四边形BEGF为平行四边形
则EF∥BG
又∵EF?平面PAB,BG?平面PAB
故EF∥平面PAB
点评:本题考查的知识点是空间中直线与平面垂直的判定及直线与平面平行的判定,其中熟练掌握空间线面垂直及线面平行的判定定理及解答方法步骤,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=