题目内容
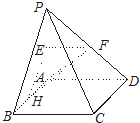如图，四棱锥P-ABCD的底面为正方形，侧棱PA⊥平面ABCD，且PA=AD=2，E、F、H分别是线段PA、PD、AB的中点．（1）求证：PD⊥平面AHF；
（2）求证：平面PBC∥平面EFH．
分析：（1）要证PD⊥平面AHF，须证PD垂直面内两条相交直线即可．
（2）要证平面PBC∥平面EFH，须证平面PBC内的两相交直线都与平面EFH平行即可．
（2）要证平面PBC∥平面EFH，须证平面PBC内的两相交直线都与平面EFH平行即可．
解答：证明：（1）因为AP=AD，且F为PD的中点，所以PD⊥AF．
因为PA⊥平面ABCD，且AH?平面ABCD，所以AH⊥PA；
因为ABCD为正方形，所以AH⊥AD；
又PA∩AD=A，所以AH⊥平面PAD．
因为PD?平面PAD，所以AH⊥PD．
又AH∩AF=A，所以PD⊥平面AHF．
（2）因为E、H分别是线段PA、AB的中点，所以EH∥PB．
又PB?平面PBC，EH?平面PBC，所以EH∥平面PBC．
因为E、F分别是线段PA、PD的中点，所以EF∥AD，
因为ABCD为正方形，所以AD∥BC，所以EF∥BC，
又BC?平面PBC，EF?平面PBC，所以EF∥平面PBC．
因为EF∩EH=E，且EF?平面EFH，EH?平面EFH，所以平面PBC∥平面EFH．
因为PA⊥平面ABCD，且AH?平面ABCD，所以AH⊥PA；
因为ABCD为正方形，所以AH⊥AD；
又PA∩AD=A，所以AH⊥平面PAD．
因为PD?平面PAD，所以AH⊥PD．
又AH∩AF=A，所以PD⊥平面AHF．
（2）因为E、H分别是线段PA、AB的中点，所以EH∥PB．
又PB?平面PBC，EH?平面PBC，所以EH∥平面PBC．
因为E、F分别是线段PA、PD的中点，所以EF∥AD，
因为ABCD为正方形，所以AD∥BC，所以EF∥BC，
又BC?平面PBC，EF?平面PBC，所以EF∥平面PBC．
因为EF∩EH=E，且EF?平面EFH，EH?平面EFH，所以平面PBC∥平面EFH．
点评：本题考查空间直线与平面之间的位置关系，平面与平面之间的位置关系，是中档题．
练习册系列答案
习题精选系列答案
相关题目
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，
如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD=2，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°，M为AP的中点．
如图，四棱锥P-ABCD的底面ABCD是矩形，AB=2，
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，且PA=AB=1，
如图，四棱锥P-ABCD，PA⊥平面ABCD，ABCD是直角梯形，DA⊥AB，CB⊥AB，PA=2AD=BC=2，AB=