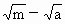题目内容
若椭圆![]() =1(m>n>0)和双曲线
=1(m>n>0)和双曲线![]() =1(a>0,b>0)有相同的焦点F1和F2,点P是两曲线的一个交点(如图所示).
=1(a>0,b>0)有相同的焦点F1和F2,点P是两曲线的一个交点(如图所示).
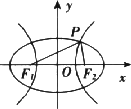
求证:(1)|PF1|·|PF2|=m2-a2;
(2)△PF1F2的面积S=nb.
答案:
解析:
提示:
解析:
|
|
提示:
|
对(2)题也可以把双曲线与椭圆方程联立求得P点坐标,然后计算 |

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目

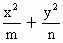 =1(m>n>0)和双曲线
=1(m>n>0)和双曲线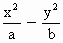 =1(a>0,b>0)有相同的焦点
=1(a>0,b>0)有相同的焦点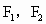 ,P是两条曲线的一个交点,则
,P是两条曲线的一个交点,则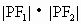 的值为
的值为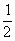 (m-a)
(m-a)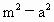 D.
D.