题目内容
已知函数![]() .
.
(1) 求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2) 求证:函数![]() 存在单调递减区间
存在单调递减区间![]() ,并求出单调递减区间的长度
,并求出单调递减区间的长度![]() 的取值范围.
的取值范围.
解:(Ⅰ)函数![]() 的定义域为
的定义域为![]() ,
,![]()
![]()
所以曲线![]() 在点
在点![]() 处的切线方程为:
处的切线方程为:![]()
(Ⅱ)![]()
![]() .
.
因为![]() 且对称轴为
且对称轴为![]() ,
,
![]() ,
,
所以方程![]() 在
在![]() 内有两个不同实根
内有两个不同实根![]() ,
,
即![]() 的解集为
的解集为![]() ,
,
所以函数![]() 的单调递减区间为
的单调递减区间为![]() .
.
![]()
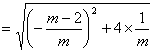
![]()
由于![]() ,所以
,所以![]()
![]() ,
,
又![]()
![]()
![]()
所以函数![]() 的递减区间长度
的递减区间长度![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
题目内容
已知函数![]() .
.
(1) 求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2) 求证:函数![]() 存在单调递减区间
存在单调递减区间![]() ,并求出单调递减区间的长度
,并求出单调递减区间的长度![]() 的取值范围.
的取值范围.
解:(Ⅰ)函数![]() 的定义域为
的定义域为![]() ,
,![]()
![]()
所以曲线![]() 在点
在点![]() 处的切线方程为:
处的切线方程为:![]()
(Ⅱ)![]()
![]() .
.
因为![]() 且对称轴为
且对称轴为![]() ,
,
![]() ,
,
所以方程![]() 在
在![]() 内有两个不同实根
内有两个不同实根![]() ,
,
即![]() 的解集为
的解集为![]() ,
,
所以函数![]() 的单调递减区间为
的单调递减区间为![]() .
.
![]()
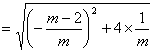
![]()
由于![]() ,所以
,所以![]()
![]() ,
,
又![]()
![]()
![]()
所以函数![]() 的递减区间长度
的递减区间长度![]() 的取值范围是
的取值范围是![]() .
.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案