题目内容
已知正项数列{an}的首项a1=m,其中0<m<1,函数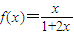 .
.(1)若数列{an}满足an+1=f(an)(n≥1且n∈N),证明
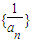 是等差数列,并求出数列{an}的通项公式;
是等差数列,并求出数列{an}的通项公式;(2)若数列{an}满足an+1≤f(an)(n≥1且n∈N),数列{bn}满足bn=
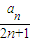 ,试证明b1+b2+…+bn<
,试证明b1+b2+…+bn< .
.
【答案】分析:本题考查数列与函数的关系、等差数列的证明、求数列的通项公式、求数列的前n项和、裂项法求和等数列知识和方法,
(1)根据所给函数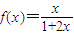 及an+1=f(an)可得数列的递推关系,由此获得
及an+1=f(an)可得数列的递推关系,由此获得 ,数列
,数列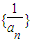 是等差
是等差
数列得证,并由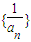 的通项公式进而得到数列{an}的通项公式;
的通项公式进而得到数列{an}的通项公式;
(2)根据{an}满足an+1≤f(an)可得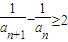 ,由此推得
,由此推得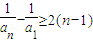 ,然后由
,然后由 即得
即得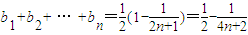 ,由此问题得证.
,由此问题得证.
解答:解:(1)∵f(x)=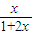
∴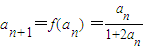
∴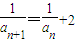
∴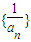 是公差为2的等差数列
是公差为2的等差数列
又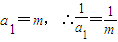
∴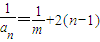
∴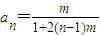
(2)由(1)知0<an+1≤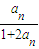
∴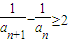
∴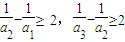 ,…,
,…,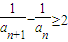 ,
,
则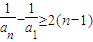
而a1=m,则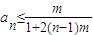
∵0<m<1,∴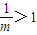
∴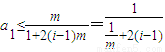 ,i=1,2,3,…,n
,i=1,2,3,…,n
∴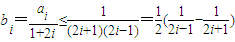 ,i=1,2,3,…,n
,i=1,2,3,…,n
∴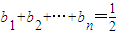 (
(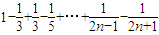 )
)
=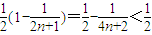 ;
;
∴b1+b2+…+bn< .
.
点评:本题综合性较强,涉及了函数与数列的关系、等差数列的证明、通项公式、求和公式等,注意解题思路分析,避免因为题意不清走了弯路,这点对于该题特别重要;
注意(2)中所使用的累加法,通过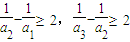 ,…,
,…,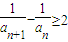 的累加,获得结果
的累加,获得结果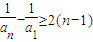 ,从而是问题得以解决;
,从而是问题得以解决;
在证明b1+b2+…+bn< 时,仍然使用了数列求和中常用的“裂项法”,使其和最终化为
时,仍然使用了数列求和中常用的“裂项法”,使其和最终化为 而得到解决.
而得到解决.
(1)根据所给函数
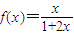 及an+1=f(an)可得数列的递推关系,由此获得
及an+1=f(an)可得数列的递推关系,由此获得 ,数列
,数列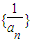 是等差
是等差数列得证,并由
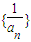 的通项公式进而得到数列{an}的通项公式;
的通项公式进而得到数列{an}的通项公式;(2)根据{an}满足an+1≤f(an)可得
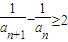 ,由此推得
,由此推得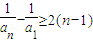 ,然后由
,然后由 即得
即得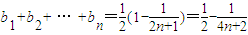 ,由此问题得证.
,由此问题得证.解答:解:(1)∵f(x)=
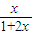
∴
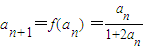
∴
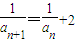
∴
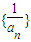 是公差为2的等差数列
是公差为2的等差数列又
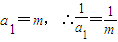
∴
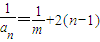
∴
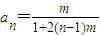
(2)由(1)知0<an+1≤
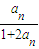
∴
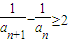
∴
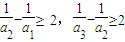 ,…,
,…,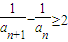 ,
,则
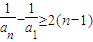
而a1=m,则
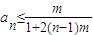
∵0<m<1,∴
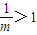
∴
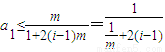 ,i=1,2,3,…,n
,i=1,2,3,…,n∴
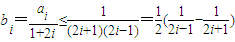 ,i=1,2,3,…,n
,i=1,2,3,…,n∴
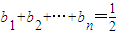 (
(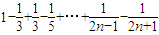 )
)=
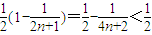 ;
;∴b1+b2+…+bn<
 .
.点评:本题综合性较强,涉及了函数与数列的关系、等差数列的证明、通项公式、求和公式等,注意解题思路分析,避免因为题意不清走了弯路,这点对于该题特别重要;
注意(2)中所使用的累加法,通过
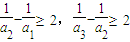 ,…,
,…,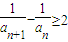 的累加,获得结果
的累加,获得结果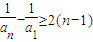 ,从而是问题得以解决;
,从而是问题得以解决;在证明b1+b2+…+bn<
 时,仍然使用了数列求和中常用的“裂项法”,使其和最终化为
时,仍然使用了数列求和中常用的“裂项法”,使其和最终化为 而得到解决.
而得到解决. 
练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目