题目内容
在数列{an}和{bn}中,a1=1,b1=2,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列(n∈N*).
(1)求a2,a3,a4和b2,b3,b4;
(2)猜想{an},{bn}的通项公式,并证明你的结论;
(3)求证: (n∈N*).
(n∈N*).
解:(1)令n=1可得2b1=a1+a2,a22=b1b2,代入条件得:
 ,解得a2=3,
,解得a2=3, ,
,
同理得a3=6,b3=8,a4=10, .(4分)
.(4分)
(2)猜想: ,
, .
.
用数学归纳法证明:
(ⅰ)当n=1时,结论显然成立
(ⅱ)假设n=k时结论成立,即 ,
,
当n=k+1时,ak+1=2bk-ak= =
= bk+1=
bk+1=
所以当n=k+1时,结论也成立
综合(ⅰ)(ⅱ)对任意n∈N*, ,bn=
,bn= 都成立.(8分)
都成立.(8分)
(3)欲证
即证
下面用数学归纳法证明:
(ⅰ)当n=1时,左=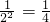 ,右=
,右= ,不等式显然成立
,不等式显然成立
(ⅱ)假设n=k时结论成立,即
当n=k+1时

而 =
=
所以
即

则n=k+1时不等式也成立.
综合(ⅰ)(ⅱ)对任意n∈N*,都有
亦即 .(12分)
.(12分)
分析:(1)令n=1可得2b1=a1+a2,a22=b1b2,代入条件求出a2,b2,同理令n=2,3即可求得a3,a4和b2,b3,b4
(2)由(1)猜想: ,
, .再利用数学归纳法证明即得;
.再利用数学归纳法证明即得;
(3)通过分析法先分析,欲证 即证
即证 ,下面用数学归纳法证明.
,下面用数学归纳法证明.
点评:本小题主要考查数列的函数特性、数列与不等式的综合、数学归纳法等基础知识,考查运算求解能力,考查化归与转化思想.利用数学归纳法证明数学命题或不等式时,要注意由归纳假设n=k成立推到n=k+1是数学归纳法的关键.
 ,解得a2=3,
,解得a2=3, ,
,同理得a3=6,b3=8,a4=10,
 .(4分)
.(4分)(2)猜想:
 ,
, .
.用数学归纳法证明:
(ⅰ)当n=1时,结论显然成立
(ⅱ)假设n=k时结论成立,即
 ,
,
当n=k+1时,ak+1=2bk-ak=
 =
= bk+1=
bk+1=
所以当n=k+1时,结论也成立
综合(ⅰ)(ⅱ)对任意n∈N*,
 ,bn=
,bn= 都成立.(8分)
都成立.(8分)(3)欲证

即证

下面用数学归纳法证明:
(ⅰ)当n=1时,左=
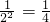 ,右=
,右= ,不等式显然成立
,不等式显然成立(ⅱ)假设n=k时结论成立,即

当n=k+1时


而
 =
=
所以

即


则n=k+1时不等式也成立.
综合(ⅰ)(ⅱ)对任意n∈N*,都有

亦即
 .(12分)
.(12分)分析:(1)令n=1可得2b1=a1+a2,a22=b1b2,代入条件求出a2,b2,同理令n=2,3即可求得a3,a4和b2,b3,b4
(2)由(1)猜想:
 ,
, .再利用数学归纳法证明即得;
.再利用数学归纳法证明即得;(3)通过分析法先分析,欲证
 即证
即证 ,下面用数学归纳法证明.
,下面用数学归纳法证明.点评:本小题主要考查数列的函数特性、数列与不等式的综合、数学归纳法等基础知识,考查运算求解能力,考查化归与转化思想.利用数学归纳法证明数学命题或不等式时,要注意由归纳假设n=k成立推到n=k+1是数学归纳法的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
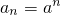 ,bn=(a+1)n+b,n=1,2,3,…,其中a≥2且a∈N*,b∈R.
,bn=(a+1)n+b,n=1,2,3,…,其中a≥2且a∈N*,b∈R.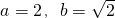 时,数列{bn}中的任意三项都不能构成等比数列.
时,数列{bn}中的任意三项都不能构成等比数列.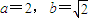 时,数列{bn}中的任意三项都不能构成等比数列;
时,数列{bn}中的任意三项都不能构成等比数列;