Question

用反证法证明:钝角三角形最大边上的中线小于该边长的一半.

Answer 1

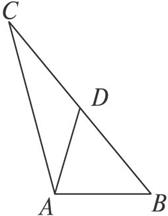
证明:已知:在△ABC中,∠CAB＞90°,D是BC的中点,求证:AD＜BC(如下图所示).

假设AD≥BC.

(1)若AD=BC,由平面几何中定理“若三角形一边上的中线等于该边长的一半,那么,这条边所对的角为直角，”知∠A=90°,与题设矛盾.所以AD≠BC.

(2)若AD＞BC,因为BD=DC=BC,所以在△ABD中,AD＞BD,从而∠B＞∠BAD,同理∠C＞∠CAD.

所以∠B+∠C＞∠BAD+∠CAD,

即∠B+∠C＞∠A.

因为∠B+∠C=180°-∠A,所以180°-∠A＞∠A,则∠A＜90°,这与题设矛盾.

由(1)(2)知AD＞BC.