题目内容
已知数列{an}的前n项和Sn满足Sn+an+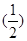 n-1=2(n∈N*),设cn=2nan.
n-1=2(n∈N*),设cn=2nan.
(1)求证:数列{cn}是等差数列,并求数列{an}的通项公式.
(2)按以下规律构造数列{bn},具体方法如下:
b1=c1,b2=c2+c3,b3=c4+c5+c6+c7,…,第n项bn由相应的{cn}中2n-1项的和组成,求数列{bn}的通项bn.
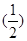 n-1=2(n∈N*),设cn=2nan.
n-1=2(n∈N*),设cn=2nan.(1)求证:数列{cn}是等差数列,并求数列{an}的通项公式.
(2)按以下规律构造数列{bn},具体方法如下:
b1=c1,b2=c2+c3,b3=c4+c5+c6+c7,…,第n项bn由相应的{cn}中2n-1项的和组成,求数列{bn}的通项bn.
(1) 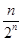 (2)
(2) 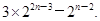
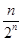 (2)
(2) 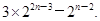
(1)证明:在Sn+an+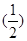 n-1=2①中,令n=1,得S1+a1+1=2,∴a1=
n-1=2①中,令n=1,得S1+a1+1=2,∴a1=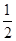
当n≥2时,Sn-1+an-1+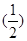 n-2=2,②
n-2=2,②
①-②得an+an-an-1-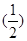 n-1=0(n≥2),
n-1=0(n≥2),
∴2an-an-1=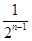 ,∴2nan-2n-1an-1=1.
,∴2nan-2n-1an-1=1.
又cn=2nan,∴cn-cn-1=1(n≥2).
又c1=2a1=1,所以,数列{cn}是等差数列.
于是cn=1+(n-1)×1=n,又∵cn=2nan,∴an=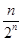 .
.
(2)解:由题意得
bn=c2n-1+c2n-1+1+c2n-1+2+…+c2n-1=2n-1+(2n-1+1)+(2n-1+2)+…+(2n-1),而2n-1,2n-1+1,2n-1+2,…,2n-1是首项为2n-1,公差为1的等差数列,且共有2n-1项,所以,bn=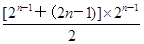 =
=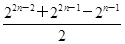 =
=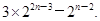
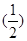 n-1=2①中,令n=1,得S1+a1+1=2,∴a1=
n-1=2①中,令n=1,得S1+a1+1=2,∴a1=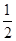
当n≥2时,Sn-1+an-1+
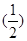 n-2=2,②
n-2=2,②①-②得an+an-an-1-
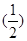 n-1=0(n≥2),
n-1=0(n≥2),∴2an-an-1=
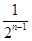 ,∴2nan-2n-1an-1=1.
,∴2nan-2n-1an-1=1.又cn=2nan,∴cn-cn-1=1(n≥2).
又c1=2a1=1,所以,数列{cn}是等差数列.
于是cn=1+(n-1)×1=n,又∵cn=2nan,∴an=
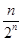 .
.(2)解:由题意得
bn=c2n-1+c2n-1+1+c2n-1+2+…+c2n-1=2n-1+(2n-1+1)+(2n-1+2)+…+(2n-1),而2n-1,2n-1+1,2n-1+2,…,2n-1是首项为2n-1,公差为1的等差数列,且共有2n-1项,所以,bn=
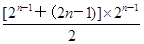 =
=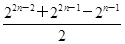 =
=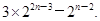

练习册系列答案
相关题目
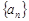 的前
的前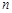 项和为
项和为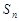 ,首项
,首项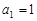 ,点
,点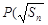 ,
,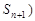 在曲线
在曲线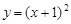 上.
上.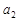 ,
,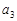 ;
;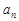 ;
;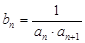 ,
,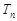 表示数列
表示数列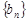 的前项和,若
的前项和,若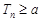 恒成立,求
恒成立,求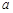 的取值范围.
的取值范围.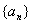 的首项
的首项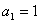 ,前
,前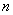 项和为
项和为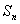 (
(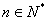 ),且点
),且点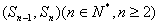 在直线
在直线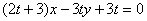 上(
上(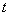 为与
为与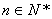 )为等比数列;
)为等比数列;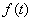 ,数列
,数列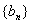 满足
满足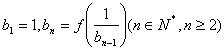 ,设
,设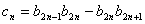 ,求数列
,求数列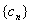 的前
的前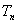 ;
;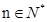 时不等式
时不等式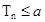 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。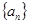 的各项均为正数,且
的各项均为正数,且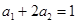 ,
,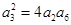 .
.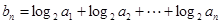 ,求数列
,求数列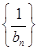 的前
的前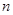 项和.
项和.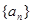 是公差不为零的等差数列,
是公差不为零的等差数列,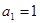 ,且
,且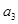 是
是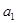 和
和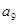 的等比中项.
的等比中项.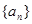 的通项公式;
的通项公式;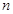 项和为
项和为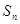 ,
,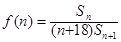 ,试问当
,试问当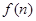 最大?并求出
最大?并求出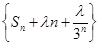 为等差数列?若存在,求出λ的值;若不存在,则说明理由.
为等差数列?若存在,求出λ的值;若不存在,则说明理由.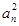 +anan+1=0,则它的通项公式为( ).
+anan+1=0,则它的通项公式为( ).