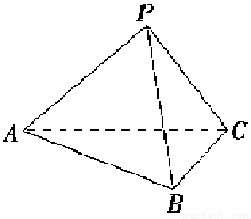
题目内容
四面体P－ABC中，已知PA＝3，PB＝PC＝2，∠APB＝∠BPC＝∠CPA＝60°.求证：
(1)PA⊥BC；
(2)平面PBC⊥平面ABC.
[解析] (1)由PB＝PC＝2，PA＝3，
∠APB＝∠BPC＝∠CPA＝60°，
得BC＝2，AC＝
，AB＝，
取CB中点F，连结AF、PF，
在等边三角形BPC中，PF⊥BC.
在等腰三角形BAC中，AF⊥BC，
∴BC⊥平面PAF，则BC⊥PA.
(2)在等边三角形BPC中，高PF＝
，BC＝2，
又PF⊥BC，∴PF⊥平面ABC，故平面PBC⊥平面ABC.
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
