Question

（2013•天津模拟）如图在四棱锥P-ABCD中，底面ABCD是边长为a的正方形，侧面PAD⊥底面ABCD，且PA=PD=

2

2

AD，设E、F分别为PC、BD的中点．
（Ⅰ） 求证：EF∥平面PAD；
（Ⅱ） 求证：面PAB⊥平面PDC；
（Ⅲ） 求二面角B-PD-C的正切值．

Answer 1

分析：（Ⅰ）利用线面平行的判定定理：连接AC，只需证明EF∥PA，利用中位线定理即可得证；
（Ⅱ）利用面面垂直的判定定理：只需证明PA⊥面PDC，进而转化为证明PA⊥PD，PA⊥DC，易证三角形PAD为等腰直角三角形，可得PA⊥PD；由面PAD⊥面ABCD的性质及正方形ABCD的性质可证CD⊥面PAD，得CD⊥PA；
（Ⅲ）设PD的中点为M，连结EM，MF，则EM⊥PD，由（Ⅱ）可证PD⊥平面EFM，则∠EMF是二面角B-PD-C的平面角，通过解Rt△FEM可得所求二面角的正切值；

解答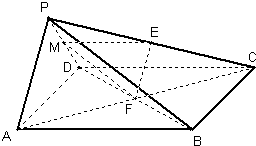：（Ⅰ）证明：ABCD为平行四边形，
连结AC∩BD=F，F为AC中点，E为PC中点，
∴在△CPA中EF∥PA，且PA?平面PAD，EF?平面PAD，
∴EF∥平面PAD；
（Ⅱ）证明：因为面PAD⊥面ABCD，平面PAD∩面ABCD=AD，ABCD为正方形，
∴CD⊥AD，CD?平面ABCD，
所以CD⊥平面PAD，∴CD⊥PA，
又PA=PD=

2

2

AD，
所以△PAD是等腰直角三角形，且∠PAD=

π

2

，即PA⊥PD，
CD∩PD=D，且CD、PD?面ABCD，PA⊥面PDC，
又PA?面PAB，
∴面PAB⊥面PDC；
（Ⅲ）解：设PD的中点为M，连结EM，MF，则EM⊥PD，
由（Ⅱ）知EF⊥面PDC，EF⊥PD，PD⊥面EFM，PD⊥MF，∠EMF是二面角B-PD-C的平面角，
Rt△FEM中，EF=

1

2

PA=

2

4

a，EM=

1

2

CD=

1

2

a，tan∠EMF=

EF

EM

=

2 4 a

1 2 a

=

2

2

，
故所求二面角的正切值为

2

2

；

点评：本题考查线面平行、面面垂直的判定及二面角的求解，考查学生的推理论证能力及逻辑思维能力，属中档题．