题目内容
已知椭圆Ω的离心率为
，它的一个焦点和抛物线y2=-4x的焦点重合．
（1）求椭圆Ω的方程；
（2）若椭圆
+
=1(a＞b＞0)上过点（x0，y0）的切线方程为
+
=1．
①过直线l：x=4上点M引椭圆Ω的两条切线，切点分别为A，B，求证：直线AB恒过定点C；
②是否存在实数λ使得|AC|+|BC|=λ•|AC|•|BC|，若存在，求出A的值；若不存在，说明理由．
| 1 |
| 2 |
（1）求椭圆Ω的方程；
（2）若椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| x0x |
| a2 |
| y0y |
| b2 |
①过直线l：x=4上点M引椭圆Ω的两条切线，切点分别为A，B，求证：直线AB恒过定点C；
②是否存在实数λ使得|AC|+|BC|=λ•|AC|•|BC|，若存在，求出A的值；若不存在，说明理由．
（1）设椭圆方程为
+
=1（a＞b＞0），
抛物线y2=-4x的焦点是（-1，0），故c=1，
又∵
=
，∴a=2，b=
=
，
∴所求的椭圆Ω的方程为
+
=1．
（2）①证明：设切点坐标为A（x1，y1），B（x2，y2），直线l上一点M的坐标（4，t），
则切线方程分别为
+
=1，
+
=1，
∵两切线均过M，即x1+
y1=1，x2+
y2=1，
即点A，B的坐标都适合方程x+
y=1
而两点之间确定的唯一的一条直线，
∴直线AB的方程是x+
=1，
对任意实数t，点（1，0）都适合这个方程，
故直线恒过定点C（1，0）．
②将直线AB的方程x+
y=1与椭圆方程联立，可得（
+4）y2-2ty-9=0
∴y1+y2=
，y1y2=
不妨设y1＞0，y2＜0，则|AC|=
=
y1
同理|BC|=-
y2
∴
+
=
•
=
即|AC|+|BC|=
•|AC|•|BC|，
故存在λ=
，使得|AC|+|BC|=λ•|AC|•|BC|．
| x2 |
| a2 |
| y2 |
| b2 |
抛物线y2=-4x的焦点是（-1，0），故c=1，
又∵
| c |
| a |
| 1 |
| 2 |
| a2-c2 |
| 3 |
∴所求的椭圆Ω的方程为
| x2 |
| 4 |
| y2 |
| 3 |
（2）①证明：设切点坐标为A（x1，y1），B（x2，y2），直线l上一点M的坐标（4，t），
则切线方程分别为
| x1x |
| 4 |
| y1y |
| 3 |
| x2x |
| 4 |
| y2y |
| 3 |
∵两切线均过M，即x1+
| t |
| 3 |
| t |
| 3 |
即点A，B的坐标都适合方程x+
| t |
| 3 |
而两点之间确定的唯一的一条直线，
∴直线AB的方程是x+
| t |
| 3 |
对任意实数t，点（1，0）都适合这个方程，
故直线恒过定点C（1，0）．
②将直线AB的方程x+
| t |
| 3 |
| t2 |
| 3 |
∴y1+y2=
| 6t |
| t2+12 |
| -27 |
| t2+12 |
不妨设y1＞0，y2＜0，则|AC|=
| (x1-1)2+y12 |
| ||
| 3 |
同理|BC|=-
| ||
| 3 |
∴
| 1 |
| |AC| |
| 1 |
| |BC| |
| 1 | ||
|
| ||
| 9 |
| 4 |
| 3 |
即|AC|+|BC|=
| 4 |
| 3 |
故存在λ=
| 4 |
| 3 |
练习册系列答案
相关题目
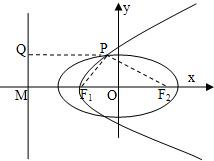已知椭圆E的离心率为e，两焦点为F1，F2，抛物线C以F1为顶点，F2为焦点，P为两曲线的一个公共点，若
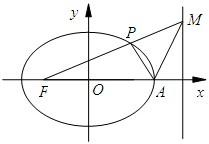如图，在平面直角坐标系xOy中，椭圆C：