题目内容
在△ABC中,角A、B、C所对的边分别为a、b、c(其中a≤b≤c),设向量 =(cosB,sinB),
=(cosB,sinB),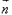 =(0,
=(0,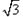 ),且向量
),且向量 为单位向量,
为单位向量,
(1)求∠B的大小;
(2)若b= ,a=1,求△ABC的面积。
,a=1,求△ABC的面积。
 =(cosB,sinB),
=(cosB,sinB),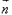 =(0,
=(0,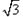 ),且向量
),且向量 为单位向量,
为单位向量,(1)求∠B的大小;
(2)若b=
 ,a=1,求△ABC的面积。
,a=1,求△ABC的面积。解:(1)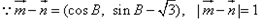 ,
,
∴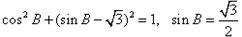 ,
,
又B为三角形的内角,
由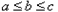 ,故
,故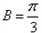 。
。
(2)根据正弦定理,知 ,即
,即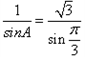 ,
,
∴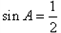 ,
,
又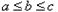 ,
,
∴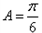 ,
,
故C=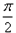 ,
,
△ABC的面积=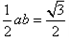 。
。
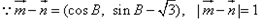 ,
,∴
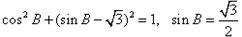 ,
,又B为三角形的内角,
由
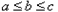 ,故
,故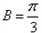 。
。(2)根据正弦定理,知
 ,即
,即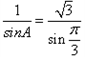 ,
,∴
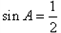 ,
,又
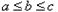 ,
,∴
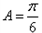 ,
,故C=
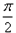 ,
,△ABC的面积=
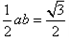 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |