Question

如图，四棱锥P-ABCD的底面ABCD是矩形，AB=2，BC=

2

，且侧面PAB是正三角形，平面PAB⊥平面ABCD，E是棱PA的中点．
（1）求证：PC∥平面EBD；
（2）求三棱锥P-EBD的体积．

Answer 1

分析：（1）连接AC，设AC、BD交点为O，利用EO是△PAC的中位线，可得PC∥EO，利用线面平行的判定，可得PC∥平面EBD；
（2）取AB中点H，先证明PH⊥平面ABCD．取AH中点F，可证EF⊥平面ABCD，进而可求三棱锥P-EBD的体积．

解答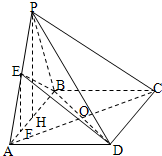：（1）证明：在矩形ABCD中，连接AC，设AC、BD交点为O，则O是AC中点．
又E是PA中点，所以EO是△PAC的中位线，所以PC∥EO…（3分）
又EO?平面EBD，PC?平面EBD．
所以PC∥平面EBD…（6分）
（2）解：取AB中点H，则由PA=PB，得PH⊥AB，
又平面PAB⊥平面ABCD，且平面PAB∩平面ABCD=AB，
所以PH⊥平面ABCD．             …．．（8分）
取AH中点F，由E是PA中点，得EF∥PH，所以EF⊥平面ABCD．
∵VP-EBD=VP-ABD-VE-ABD=

1

3

S△ABD•PH-

1

3

S△ABD•EF，
由题意可求得：S_△ABD=

2

，PH=

3

，EF=

3

2

，…．．（10分）
则VP-EBD=

1

3

×

2

×

3

-

1

3

×

2

×

3

2

=

6

6

．          …．．（12分）

点评：本题考查线面平行、线面垂直，考查三棱锥体积的计算，掌握线面平行、线面垂直的判定是解题的关键．