题目内容
中心在原点,焦点在x轴上的一个椭圆与一个双曲线有共同的焦点F1,F2,|F1F2|=2
,椭圆的长半轴与双曲线实半轴之差为4,离心率之比为3:7,
(1)求这两曲线方程;
(2)若P为两曲线的交点(P在第一象限),求
•
的值.
| 13 |
(1)求这两曲线方程;
(2)若P为两曲线的交点(P在第一象限),求
| PF1 |
| PF2 |
分析:(1)根据半焦距c=
,设椭圆长半轴为a,由离心率之比求出a,进而求出椭圆短半轴的长及双曲线的虚半轴的长,写出椭圆和双曲线的标准方程.
(2)由椭圆、双曲线的定义求出PF1与PF2的长,三角形F1PF2中,利用余弦定理求出 cos∠F1PF2 的值,最后利用向量的数量积公式求解即可.
| 13 |
(2)由椭圆、双曲线的定义求出PF1与PF2的长,三角形F1PF2中,利用余弦定理求出 cos∠F1PF2 的值,最后利用向量的数量积公式求解即可.
解答:解:(1)由题意知,半焦距c=
,设椭圆长半轴为a,则双曲线实半轴 a-4,
离心率之比为
=
,
∴a=7,
∴椭圆的短半轴等于
=6,双曲线虚半轴的长为
=2,
∴椭圆和双曲线的方程分别为:
+
=1和
-
=1.
(2)由椭圆的定义得:PF1 +PF2=2a=14,
由双曲线的定义得:PF1-PF2=6,
∴PF1=10,PF2=4,
又F1F2=2
,三角形F1PF2中,利用余弦定理得:(2
)2=100+16-80cos∠F1PF2,
∴cos∠F1PF2=
.
则
•
=|
|•|
|cos∠F1PF2=10×4×
=32.
| 13 |
离心率之比为
| 3 |
| 7 |
| ||||
|
∴a=7,
∴椭圆的短半轴等于
| 49-13 |
| 13-9 |
∴椭圆和双曲线的方程分别为:
| x2 |
| 49 |
| y2 |
| 36 |
| x2 |
| 9 |
| y2 |
| 4 |
(2)由椭圆的定义得:PF1 +PF2=2a=14,
由双曲线的定义得:PF1-PF2=6,
∴PF1=10,PF2=4,
又F1F2=2
| 13 |
| 13 |
∴cos∠F1PF2=
| 4 |
| 5 |
则
| PF1 |
| PF2 |
| PF1 |
| PF2 |
| 4 |
| 5 |
点评:本题主要考查椭圆、双曲线的标准方程和几何性质、平面向量数量积的运算,考查计算能力.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
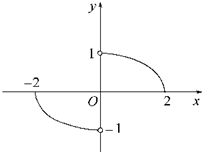 如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{x|-
| ||||||||
B、{x|-2≤x<-
| ||||||||
C、{x|-2≤x<-
| ||||||||
D、{x|-
|
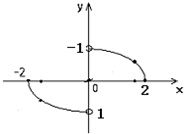 如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{
| ||||||||
B、{x|-2≤x<
| ||||||||
C、{x|-
| ||||||||
D、{x|-
|
 .
.