题目内容
函数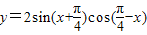 图象的一个对称轴方程是( )
图象的一个对称轴方程是( )A.
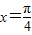
B.
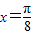
C.
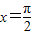
D.x=π
【答案】分析:将函数解析式最后一个因式中的角变形后,利用诱导公式化简,再利用二倍角的余弦函数公式化简,最后利用诱导公式化为一个角的正弦函数,由正弦函数的图象与性质即可得出函数y的对称轴方程,进而确定出正确的选项.
解答:解:y=2sin(x+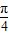 )cos(
)cos(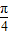 -x)=2sin(x+
-x)=2sin(x+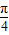 )cos[
)cos[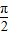 -(x+
-(x+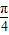 )]=2sin2(x+
)]=2sin2(x+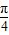 )=1-cos(2x+
)=1-cos(2x+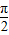 )=1+sin2x,
)=1+sin2x,
令2x=2kπ+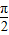 ,k∈Z,得到x=kπ+
,k∈Z,得到x=kπ+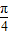 ,k∈Z,
,k∈Z,
则k=1时,x=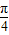 为函数的一个对称轴方程.
为函数的一个对称轴方程.
故选A
点评:此题考查了诱导公式,二倍角的余弦函数公式,以及正弦函数的对称性,熟练掌握公式是解本题的关键.
解答:解:y=2sin(x+
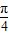 )cos(
)cos(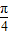 -x)=2sin(x+
-x)=2sin(x+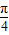 )cos[
)cos[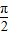 -(x+
-(x+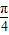 )]=2sin2(x+
)]=2sin2(x+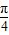 )=1-cos(2x+
)=1-cos(2x+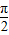 )=1+sin2x,
)=1+sin2x,令2x=2kπ+
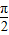 ,k∈Z,得到x=kπ+
,k∈Z,得到x=kπ+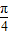 ,k∈Z,
,k∈Z,则k=1时,x=
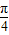 为函数的一个对称轴方程.
为函数的一个对称轴方程.故选A
点评:此题考查了诱导公式,二倍角的余弦函数公式,以及正弦函数的对称性,熟练掌握公式是解本题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 图象的一个对称轴方程是( )
图象的一个对称轴方程是( )


 图象的一个对称轴方程是( )
图象的一个对称轴方程是( )


 图象的一个对称轴方程是( )
图象的一个对称轴方程是( )


 图象的一个对称轴方程是( )
图象的一个对称轴方程是( )


 图象的一个对称轴方程是( )
图象的一个对称轴方程是( )

