题目内容
已知函数f(x)=loga(x+b)(其中a,b为常数,且a>0,a≠1)的图象经过点A(1,2),B(-1,1).
(1)求f(x)的解析式;
(2)若函数g(x)=( )2x-(
)2x-( )x-1,x∈[0,+∞),求g(x)的值域.
)x-1,x∈[0,+∞),求g(x)的值域.
解:(1)把A(1,2),B(-1,1).代入f(x)=loga(x+b)得 .
.
结合a>0,a≠1,解得a=2,b=3,故f(x)=log2(x+3).
(2)由(1)知a=2,b=3,∴ .
.
令 ,0<t≤1,∴
,0<t≤1,∴ ,
,
当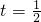 时g(t)取最小值
时g(t)取最小值 ;当t=1时,g(t)取最大值-1.
;当t=1时,g(t)取最大值-1.
因此g(t)的值域为 .
.
分析:(1)把A(1,2),B(-1,1).代入函数f(x)=loga(x+b),解得a和b的值,即可求得函数f(x)的解析式.
(2)由(1)知 .令
.令 ,0<t≤1,可得
,0<t≤1,可得 ,再利用二次函数的性质
,再利用二次函数的性质
求得g(t)的最值,即可得到它的值域.
点评:本题主要考查用待定系数法求函数的解析式,对数函数的退昂和性质的综合应用,利用二次函数的性质求函数的最值,属于中档题.
 .
.结合a>0,a≠1,解得a=2,b=3,故f(x)=log2(x+3).
(2)由(1)知a=2,b=3,∴
 .
.令
 ,0<t≤1,∴
,0<t≤1,∴ ,
,当
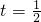 时g(t)取最小值
时g(t)取最小值 ;当t=1时,g(t)取最大值-1.
;当t=1时,g(t)取最大值-1.因此g(t)的值域为
 .
.分析:(1)把A(1,2),B(-1,1).代入函数f(x)=loga(x+b),解得a和b的值,即可求得函数f(x)的解析式.
(2)由(1)知
 .令
.令 ,0<t≤1,可得
,0<t≤1,可得 ,再利用二次函数的性质
,再利用二次函数的性质求得g(t)的最值,即可得到它的值域.
点评:本题主要考查用待定系数法求函数的解析式,对数函数的退昂和性质的综合应用,利用二次函数的性质求函数的最值,属于中档题.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目